6 Four Examples

This chapter treats four examples of non-trivial statistical models in some detail. These are all parametric models, and a central computational challenge is to fit the models to data via (penalized) likelihood maximization. The actual optimization algorithms and implementations are the topics of Chapters 7 and 8. The focus of this chapter is on the structure of the statistical models themselves to provide the necessary background for the later chapters.

Statistical models come in all forms and shapes, and it is possible to take a very general and abstract mathematical approach; statistical models are parametrized families of probability distributions. To say anything of interest, we need more structure such as structure on the parameter set, properties of the parametrized distributions, and properties of the mapping from the parameter set to the distributions. For any specific model we have ample of structure but often also an overwhelming amount of irrelevant details that will be more distracting than clarifying. The intention is that the four examples treated will illustrate the breath of statistical models that share important structures without getting lost in a wasteland of abstractions.

If one should emphasize a single abstract idea that is of theoretical value as well as of practical importance, it is the idea of exponential families. Statistical models that are exponential families have so much structure that the general theory provides a number of results and details of practical value for individual models. Exponential families are exemplary statistical models, that are widely used as models of data, or as central building blocks of more complicated models of data. For this reason, the treatment of the examples is preceded by a treatment of exponential families.

6.1 Exponential families

This section introduces exponential families in a concise way. The crucial observation is that the log-likelihood is concave, and that we can derive general formulas for derivatives. This will be important for the optimization algorithms developed later for computing maximum-likelihood estimates and for answering standard asymptotic inference questions.

The exponential families are extremely well behaved from a mathematical as well as a computational viewpoint, but they may be inadequate for modeling data in some cases. A typical practical problem is that there is heterogeneous variation in data beyond what can be captured by any single exponential family. A fairly common technique is then to build an exponential family model of the observed variables as well as some latent variables. The latent variables then serve the purpose of modeling the heterogeneity. The resulting model of the observed variables is consequently the marginalization of an exponential family, which is generally not an exponential family and in many ways less well behaved. It is nevertheless possible to exploit the exponential family structure underlying the marginalized model for many computations of statistical importance. The EM-algorithm as treated in Chapter 8 is one particularly good example, but Bayesian computations can in similar ways exploit the structure.

6.1.1 Full exponential families

In this section we consider statistical models on an abstract product sample space \[\mathcal{Y} = \mathcal{Y}_1 \times \ldots \times \mathcal{Y}_m.\] We will be interested in models of observations \(y_1 \in \mathcal{Y}_1, \ldots, y_m \in \mathcal{Y}_m\) that are independent but not necessarily identically distributed.

An exponential family is defined in terms of two ingredients:

• maps \(t_j : \mathcal{Y}_j \to \mathbb{R}^p\) for \(j = 1, \ldots, m\),
• and non-trivial \(\sigma\)-finite measures \(\nu_j\) on \(\mathcal{Y}_j\) for \(j = 1, \ldots, m\).

The maps \(t_j\) are called sufficient statistics, and in terms of these and the base measures \(\nu_j\) we define \[\varphi_j(\theta) = \int e^{\theta^T t_j(u)} \nu_j(\mathrm{d}u).\] These functions are well defined as functions \[\varphi_j : \mathbb{R}^p \to (0,\infty].\] We define \[\Theta_j = \mathrm{int}(\{ \theta \in \mathbb{R}^p \mid \varphi_j(\theta) < \infty \}),\] which by definition is an open set as. It can be shown that \(\Theta_j\) is convex and that \(\varphi_j\) is a log-convex function. Defining \[\Theta = \bigcap_{j=1}^m \Theta_j,\] then \(\Theta\) is likewise open and convex, and we define the exponential family as the distributions parametrized by \(\theta \in \Theta\) that have densities

\[\begin{equation} f(\mathbf{y} \mid \theta) = \prod_{j=1}^m \frac{1}{\varphi_j(\theta)} e^{\theta^T t_j(y_j)} = e^{\theta^T \sum_{j=1}^m t_j(y_j) - \sum_{j=1}^m \log \varphi_j(\theta)}, \quad \mathbf{y} \in \mathcal{Y}, \tag{6.1} \end{equation}\]

w.r.t. \(\otimes_{j=1}^m \nu_j\). The case where \(\Theta = \emptyset\) is of no interest, and we will thus assume that the parameter set \(\Theta\) is non-empty. The parameter \(\theta\) is called the canonical parameter and \(\Theta\) is the canonical parameter space. We may also say that the exponential family is canonically parametrized by \(\theta\). It is important to realize that an exponential family may come with a non-canonical parametrization that doesn’t reveal right away that it is an exponential family. Thus a bit of work is then needed to show that the parametrized family of distributions can, indeed, be reparametrized as an exponential family. In the non-canonical parametrization, the family is then an example of a curved exponential family as defined below.

Example 6.1 The von Mises distributions on \(\mathcal{Y} = (-\pi, \pi]\) form an exponential family with \(m = 1\). The sufficient statistic \(t_1 : (-\pi, \pi] \mapsto \mathbb{R}^2\) is \[t_1(y) = \left(\begin{array}{c} \cos(y) \\ \sin(y) \end{array}\right),\] and \[\varphi(\theta) = \int_{-\pi}^{\pi} e^{\theta_1 \cos(u) + \theta_2 \sin(u)} \mathrm{d}u < \infty\] for all \(\theta = (\theta_1, \theta_2)^T \in \mathbb{R}^2\). Thus the canonical parameter space is \(\Theta = \mathbb{R}^2\).

As mentioned in Section 1.2.1, the function \(\varphi(\theta)\) can be expressed in terms of a modified Bessel function, but it doesn’t have an expression in terms of elementary functions. Likewise in Section 1.2.1, an alternative parametrization (polar coordinates) was given; \[(\kappa, \mu) \mapsto \theta = \kappa \left(\begin{array}{c} \cos(\mu) \\ \sin(\mu) \end{array}\right)\] that maps \([0,\infty) \times (-\pi, \pi]\) onto \(\Theta\). The von Mises distributions form a curved exponential family in the \((\kappa, \mu)\)-parametrization, but this parametrization has several problems. First, the \(\mu\) parameter is not identifiable if \(\kappa = 0\), which is reflected by the fact that the reparametrization is not a one-to-one map. Second, the parameter space is not open, which can be quite a nuisance for e.g. maxmimum-likelihood estimation. We could circumvent these problems by restricting attention to \((\kappa, \mu) \in (0,\infty) \times (-\pi, \pi)\), but we would then miss some of the distributions in the exponential family – notably the uniform distribution corresponding to \(\theta = 0\). In conclusion, the canonical parametrization of the family of distributions as an exponential family is preferable for mathematical and computational reasons.

Example 6.2 The family of Gaussian distributions on \(\mathbb{R}\) is an example of an exponential family as defined above with \(m = 1\) and \(\mathcal{Y} = \mathbb{R}\). The density of the \(\mathcal{N}(\mu, \sigma^2)\) distribution is \[\frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{(y - \mu)^2}{2\sigma^2}\right) = \frac{1}{\sqrt{\pi}} \exp\left(\frac{\mu}{\sigma^2} y - \frac{1}{2\sigma^2} y^2 - \frac{\mu^2}{2\sigma^2} - \frac{1}{2}\log (2\sigma^2) \right).\] Letting the base measure \(\nu_1\) be Lebesgue measure scaled by \(1/\sqrt{\pi}\), and \(t_1 : \mathbb{R} \mapsto \mathbb{R}^2\) be \[t_1(y) = \left(\begin{array}{c} y \\ - y^2 \end{array}\right)\] we identify this family of distributions as an exponential family with canonical parameter \[\theta = \left(\begin{array}{c} \frac{\mu}{\sigma^2} \\ \frac{1}{2 \sigma^2} \end{array}\right).\]

We can express the mean and variance in terms of \(\theta\) as \[\sigma^2 = \frac{1}{2\theta_2} \quad \text{and} \quad \mu = \frac{\theta_1}{2\theta_2},\] and we find that \[\log \varphi_1(\theta) = \frac{\mu^2}{2\sigma^2} + \frac{1}{2} \log(2 \sigma^2) = \frac{\theta_1^2}{4\theta_2} - \frac{1}{2} \log \theta_2.\]

We note that the reparametrization \((\mu, \sigma^2) \mapsto \theta\) maps \(\mathbb{R} \times (0,\infty)\) bijectively onto the open set \(\mathbb{R} \times (0,\infty)\), and that the formula above for \(\log \varphi_1(\theta)\) only holds on this set. It is natural to ask if the canonical parameter space is actually larger for this exponential family. That is, is \(\varphi_1(\theta) < \infty\) for \(\theta_2 \leq 0\)? To this end observe that if \(\theta_2 \leq 0\) \[\varphi_1(\theta) = \frac{1}{\sqrt{2\pi}} \int e^{\theta_1 u - \theta_2 \frac{u^2}{2}} \mathrm{d}u \geq \frac{1}{\sqrt{2\pi}} \int e^{\theta_1 u} \mathrm{d} u = \infty,\] and we conclude that \[\Theta = \mathbb{R} \times (0,\infty).\]

The family of Gaussian distributions is an example of a family of distributions whose commonly used parametrization in terms of mean and variance differs from the canonical parametrization as an exponential family. The mean and variance are easy to interpret, but in terms of mean and variance, the Gaussian distributions form a curved exponential family. For mathematical and computational purposes the canonical parametrization is preferable.

For general exponential families it may seem restrictive that all the sufficient statistics, \(t_j\), take values in the same \(p\)-dimensional space, and that all marginal distributions share a common parameter vector \(\theta\). This is, however, not a restriction. Say we have two distributions with sufficient statistics \(\tilde{t}_1 : \mathcal{Y}_1 \to \mathbb{R}^{p_1}\) and \(\tilde{t}_2 : \mathcal{Y}_2 \to \mathbb{R}^{p_2}\) and corresponding parameters \(\theta_1\) and \(\theta_2\), then we construct \[t_1(y_1) = \left(\begin{array}{c} \tilde{t}_1(y_1) \\ 0 \end{array}\right) \quad \text{and} \quad t_2(y_2) = \left(\begin{array}{c} 0 \\ \tilde{t}_2(y_2) \end{array}\right).\] Now \(t_1\) and \(t_2\) both map into \(\mathbb{R}^{p}\) with \(p = p_1 + p_2\), and we can bundle the parameters together into the vector \[\theta = \left(\begin{array}{c} \theta_1 \\ \theta_2 \end{array}\right) \in \mathbb{R}^p.\] Clearly, this construction can be generalized to any number of distributions and allows us to always assume a common parameter space. The sufficient statistics then take care of selecting which of the coordinates in the parameter vector that is used for any particular marginal distribution.

6.1.2 Exponential family Bayesian networks

An exponential family is defined above as a parametrized family of distributions on \(\mathcal{Y}\) of independent variables. That is, the joint density in (6.1) factorizes w.r.t. a product measure. Without really changing the notation this assumption can be relaxed considerably.

If the sufficient statistic \(t_j\), instead of being a fixed map, is allowed to depend on \(y_1, \ldots, y_{j-1}\), \(f(\mathbf{y} \mid \theta)\) as defined in (6.1) is still a joint density. The only difference is that the factor \[f_j(y_j \mid y_1, \ldots, y_{j-1}, \theta) = e^{\theta^T t_j(y_j) - \log \varphi_j(\theta)}\] is now the conditional density of \(y_j\) given \(y_1, \ldots, y_{j-1}\). In the notation we let the dependence of \(t_j\) on \(y_1, \ldots, y_{j-1}\) be implicit as this will not affect the abstract theory. In any concrete example though, it will be clear how \(t_j\) actually depends upon all, some or none of these variables. Note that \(\varphi_j\) may now also depend upon the data through \(y_1, \ldots, y_{j-1}\).

The observation above is powerful. It allows us to develop a unified approach based on exponential families for a majority of all statistical models that are applied in practice. The models we consider make two essential assumptions

1. the variables that we model can be ordered such that \(y_j\) only depends on \(y_1, \ldots, y_{j-1}\) for \(j = 1, \ldots, m\),
2. all the conditional distributions form exponential families themselves, with the conditioning variables entering through the \(t_j\)-maps.

The first of these assumptions is equivalent to the joint distribution being a Bayesian network, that is, a distribution whose density factorizes according to a directed acyclic graph. This includes time series models and hierarchical models. The second assumption is more restrictive, but is a common practice in applied work. Moreover, as many standard statistical models of univariate discrete and continuous variables are, in fact, exponential families, building up a joint distribution as a Bayesian network via conditional binomial, Poisson, beta, Gamma and Gaussian distributions among others is a rather flexible framework, and yet it will result in a model with a density that factorizes as in (6.1).

Bayesian networks is a large and interesting subject in itself, and it is unfair to gloss over all the details. One of the main points is that for many computations it is possible to develop efficient algorithms by exploiting the graph structure. The seminal paper by Lauritzen and Spiegelhalter (1988) demonstrated this for the computation of conditional distributions. The mere fact that the variables can be ordered in a way that aligns with how the variables depend on each other is useful, but there can be many ways to do this, and just specifying an ordering ignores important details of the graph. It is, however, beyond the scope of this book to get into the graph algorithms required for a thorough general treatment of Bayesian networks.

6.1.3 Likelihood computations

To simplify the notation we introduce \[t(\mathbf{y}) = \sum_{j=1}^m t_j(y_j),\] which we refer to as the sufficient statistic, and \[\kappa(\theta) = \sum_{j=1}^m \log \varphi_j(\theta),\] which is a convex \(C^{\infty}\)-function on \(\Theta\).

Having observed \(\mathbf{y} \in \mathcal{Y}\) it is evident that the log-likelihood for the exponential family specified by (6.1) is \[\ell(\theta) = \log f(\mathbf{y} \mid \theta) = \theta^T t(\mathbf{y}) - \kappa(\theta).\] From this it follows that the gradient of the log-likelihood is \[\nabla \ell(\theta) = t(\mathbf{y}) - \nabla \kappa(\theta)\] and the Hessian is \[D^2 \ell(\theta) = - D^2 \kappa(\theta),\] which is always negative semidefinite. The maximum-likelihood estimator exists if and only if there is a solution to the score equation \[t(\mathbf{y}) = \nabla \kappa(\theta),\] and it is unique if there is such a solution, \(\hat{\theta}\), for which \(I(\hat{\theta}) = D^2 \kappa(\hat{\theta})\) is positive definite. We call \(I(\hat{\theta})\) the observed Fisher information.

Note that under the independence assumption, \[\nabla \log \varphi_j(\theta) = \frac{1}{\varphi_j(\theta)} \int t_j(u) e^{\theta^T t_j(u)} \nu_i(\mathrm{d} u) = E_{\theta}(t_j(Y)), \] which means that the score equation can be expressed as \[t(\mathbf{y}) = \sum_{j=1}^m E_{\theta}(t_j(Y)).\] In the Bayesian network setup \(\nabla \log \varphi_j(\theta) = E_{\theta}(t_j(Y) \mid Y_1, \ldots, Y_{j-1}),\) and the score equation is \[t(\mathbf{y}) = \sum_{j=1}^m E_{\theta}(t_j(Y) \mid y_1, \ldots, y_{j-1}),\] which is a bit more complicated as the right-hand-side depends on the observations.

The definition of an exponential family in Section 6.1 encompasses the situation where \(y_1, \ldots, y_m\) are i.i.d. by taking \(t_j\) to be independent of \(j\). In that case, \(\kappa(\theta) = m \kappa_1(\theta)\), the score equation can be rewritten as \[\frac{1}{m} \sum_{j=1}^m t_1(y_j) = \kappa_1(\theta),\] and the Fisher information becomes \[I(\hat{\theta}) = m D^2 \kappa_1(\hat{\theta}).\]

However, the point of the general formulation is that it includes regression models, and, via the Bayesian networks extension above, models with dependence structures. We could, of course, then have i.i.d. replications \(\mathbf{y}_1, \ldots, \mathbf{y}_n\) of the entire \(m\)-dimensional vector \(\mathbf{y}\), and we would get the score equation \[\frac{1}{n} \sum_{i=1}^n t(\mathbf{y}_i) = \kappa(\theta),\] and corresponding Fisher information \[I(\hat{\theta}) = n D^2 \kappa(\hat{\theta}).\]

6.1.4 Curved exponential families

A curved exponential family consists of an exponential family together with a \(C^2\)-map \(\theta : \Psi \to \Theta\) from a set \(\Psi \subseteq \mathbb{R}^q\). The set \(\Psi\) provides a parametrization of the subset \(\theta(\Psi) \subseteq \Theta\) of the full exponential family, and the log-likelihood in the \(\psi\)-parameter is \[\ell(\psi) = \theta(\psi)^T t(\mathbf{y}) - \kappa(\theta(\psi)).\] It has gradient \[\nabla \ell(\psi) = D \theta(\psi)^T t(\mathbf{y}) - \nabla \kappa(\theta(\psi)) D \theta(\psi)\] and Hessian \[D^2 \ell(\psi) = \sum_{k=1}^p D^2\theta_k(\psi) (t(\mathbf{y})_k - \partial_k \kappa(\theta(\psi))) - D \theta(\psi)^T D^2 \kappa(\theta(\psi)) D \theta(\psi).\]

6.2 Multinomial models

The multinomial model is the model of all probability distributions on a finite set \(\mathcal{Y} = \{1, \ldots, K\}\). The model is parametrized by the simplex \[\Delta_K = \left\{(p_1, \ldots, p_K)^T \in \mathbb{R}^K \mid p_k \geq 0, \sum_{k=1}^K p_k = 1\right\}.\] The distributions parametrized by the relative interior of \(\Delta_K\) form an exponential family by the parametrization \[p_k = \frac{e^{\theta_k}}{\sum_{l=1}^K e^{\theta_l}} \in (0,1)\] for \((\theta_1, \ldots, \theta_K)^T \in \mathbb{R}^K.\) That is, the sufficient statistic is \(k \mapsto (\delta_{1k}, \ldots, \delta_{Kk})^T \in \mathbb{R}^{K-1}\) (where \(\delta_{lk} \in \{0, 1\}\) is the Kronecker delta being 1 if and only if \(l = k\)), and \[\varphi(\theta_1, \ldots, \theta_K) = \sum_{l=1}^K e^{\theta_l}.\] We call this exponential family parametrization the symmetric parametrization. The canonical parameter in the symmetric parametrization is not identifiable, and to resolve the lack of identifiability there is a tradition of fixing the last parameter as \(\theta_K = 0\). This results in a canonical parameter \(\theta = (\theta_1, \ldots, \theta_{K-1})^T \in \mathbb{R}^{K-1},\) a sufficient statistic \(t_1(k) = (\delta_{1k}, \ldots, \delta_{(K-1)k})^T \in \mathbb{R}^p\),

\[\varphi(\theta) = 1 + \sum_{l=1}^{K-1} e^{\theta_l}\]

and probabilities

\[p_k = \left\{\begin{array}{ll} \frac{e^{\theta_k}}{1 + \sum_{l=1}^{K-1} e^{\theta_l}} & \quad \text{if } k = 1, \ldots, K-1 \\ \frac{1}{1 + \sum_{l=1}^{K-1} e^{\theta_l}} & \quad \text{if } k = K. \end{array}\right.\]

We see that in this parametrization \(p_k = e^{\theta_k}p_K\) for \(k = 1, \ldots, K-1\), where the probability of the last element \(K\) acts as a baseline or reference probability, and the factors \(e^{\theta_k}\) act as multiplicative modifications of this baseline. Moreover, \[\frac{p_k}{p_l} = e^{\theta_k - \theta_l},\] which is independent of the chosen baseline.

In the special case of \(K = 2\) the two elements \(\mathcal{Y}\) are often given other labels than \(1\) and \(2\). The most common labels are \(\{0, 1\}\) and \(\{-1, 1\}\). If we use the \(0\)-\(1\)-labels the convention is to use \(p_0\) as the baseline and thus \[p_1 = \frac{e^{\theta}}{1 + e^{\theta}} = e^{\theta} p_0 = e^{\theta} (1 - p_1).\] parametrized by \(\theta \in \mathbb{R}\). As this function of \(\theta\) is known as the logistic function, this parametrization of the probability distributions on \(\{0,1\}\) is often referred to as the logistic model. From the above we see directly that \[\theta = \log \frac{p_1}{1 - p_1}\] is the log-odds.

If we use the \(\pm 1\)-labels, an alternative exponential family parametrization is \[p_k = \frac{e^{k\theta}}{e^\theta + e^{-\theta}}\] for \(\theta \in \mathbb{R}\) and \(k \in \{-1, 1\}\). This gives a symmetric treatment of the two labels while retaining the identifiability.

With i.i.d. observations from a multinomial distribution we find that the log-likelihood is

\[\begin{align*} \ell(\theta) & = \sum_{i=1}^n \sum_{k=1}^K \delta_{k y_i} \log(p_k(\theta)) \\ & = \sum_{k=1}^K \underbrace{\sum_{i=1}^n \delta_{k y_i}}_{= n_k} \log(p_k(\theta)) \\ & = \theta^T \mathbf{n} - n \log \left(1 + \sum_{l=1}^{K-1} e^{\theta_l} \right). \end{align*}\]

where \(\mathbf{n} = (n_1, \ldots, n_K)^T = \sum_{i=1}^n t(y_i)\) is the sufficient statistic, which is simply a tabulation of the times the different elements in \(\{1, \ldots, K\}\) were observed.

6.2.1 Peppered Moths

This example is on the color of the peppered Moth (Birkemåler in Danish). The color of the moth is primarily determined by one gene that occur in three different alleles denoted C, I and T. The alleles are ordered in terms of dominance as C > I > T. Moths with genotype including C are dark. Moths with genotype TT are light colored. Moths with genotypes II and IT are mottled. Thus there a total of six different genotypes (CC, CI, CT, II, IT and TT) and three different phenotypes (black, mottled, light colored).

The peppered moth provided an early demonstration of evolution in the 19th century England, where the light colored moth was outnumbered by the dark colored variety. The dark color became dominant due to the increased pollution, where trees were darkened by soot, and had for that reason a selective advantage. There is a nice collection of moth in different colors at the Danish Zoological Museum, and further explanation of the role it played in understanding evolution.

We denote the allele frequencies \(p_C\), \(p_I\), \(p_T\) with \(p_C + p_I + p_T = 1.\) According to the Hardy-Weinberg principle, the genotype frequencies are then

\[p_C^2, 2p_Cp_I, 2p_Cp_T, p_I^2, 2p_Ip_T, p_T^2.\]

If we could observe the genotypes, the complete multinomial log-likelihood would be

\[\begin{align*} & 2n_{CC} \log(p_C) + n_{CI} \log (2 p_C p_I) + n_{CT} \log(2 p_C p_I) \\ & \ \ + 2 n_{II} \log(p_I) + n_{IT} \log(2p_I p_T) + 2 n_{TT} \log(p_T) \\ & = 2n_{CC} \log(p_C) + n_{CI} \log (2 p_C p_I) + n_{CT} \log(2 p_C p_I) \\ & \ \ + 2 n_{II} \log(p_I) + n_{IT} \log(2p_I (1 - p_C - p_I)) + 2 n_{TT} \log(1 - p_C - p_I). \end{align*}\]

The log-likelihood is given in terms of the genotype counts and the two probability parameters \(p_C, p_I \geq 0\) with \(p_C + p_I \leq 1\), and on the interior of this parameter set the model is a curved exponential family.

Collecting moths and determining their color will, however, only identify their phenotype, not their genotype. Thus we observe \((n_C, n_T, n_I)\), where \[n = \underbrace{n_{CC} + n_{CI} + n_{CT}}_{= n_C} + \underbrace{n_{IT} + n_{II}}_{=n_I} + \underbrace{n_{TT}}_{=n_T}.\]

For maximum-likelihood estimation of the parameters in this model from the observation \((n_C, n_T, n_I)\), we need the likelihood, that is, the likelihood in the marginal distribution of the observed variables.

The peppered Moth example is an example of cell collapsing in a multinomial model. In general, let \(A_1 \cup \ldots \cup A_{K_0} = \{1, \ldots, K\}\) be a partition and let \[M : \mathbb{N}_0^K \to \mathbb{N}_0^{K_0}\] be the map given by \[M((n_1, \ldots, n_K))_j = \sum_{k \in A_j} n_k.\]

If \(Y \sim \textrm{Mult}(p, n)\) with \(p = (p_1, \ldots, p_K)\) then \[X = M(Y) \sim \textrm{Mult}(M(p), n).\] If \(\theta \mapsto p(\theta)\) is a parametrization of the cell probabilities the log-likelihood under the collapsed multinomial model is generally

\[\begin{equation} \ell(\theta) = \sum_{j = 1}^{K_0} x_j \log (M(p(\theta))_j) = \sum_{j = 1}^{K_0} x_j \log \left(\sum_{k \in A_j} p_k(\theta)\right). \tag{6.2} \end{equation}\]

For the peppered Moths, \(K = 6\) corresponding to the six genotypes, \(K_0 = 3\) and the partition corresponding to the phenotypes is \[\{1, 2, 3\} \cup \{4, 5\} \cup \{6\} = \{1, \ldots, 6\},\] and \[M(n_1, \ldots, n_6) = (n_1 + n_2 + n_3, n_4 + n_5, n_6).\]

In terms of the \((p_C, p_I)\) parametrization, \(p_T = 1 - p_C - p_I\) and \[p = (p_C^2, 2p_Cp_I, 2p_Cp_T, p_I^2, 2p_Ip_T, p_T^2).\]

Hence \[M(p) = (p_C^2 + 2p_Cp_I + 2p_Cp_T, p_I^2 +2p_Ip_T, p_T^2).\]

The log-likelihood is

\[\begin{align} \ell(p_C, p_I) & = n_C \log(p_C^2 + 2p_Cp_I + 2p_Cp_T) + n_I \log(p_I^2 +2p_Ip_T) + n_T \log (p_T^2). \end{align}\]

We can implement the log-likelihood in a very problem specific way. Note how the parameter constraints are encoded via the return value \(\infty\).

## par = c(pC, pI), pT = 1 - pC - pI
## x is the data vector of length 3 of counts 
loglik <- function(par, x) {
  pT <- 1 - par[1] - par[2]
  
  if (par[1] > 1 || par[1] < 0 || par[2] > 1 
      || par[2] < 0 || pT < 0)
    return(Inf)
  
  PC <- par[1]^2 + 2 * par[1] * par[2] + 2 * par[1] * pT
  PI <- par[2]^2 + 2 * par[2] * pT
  PT <- pT^2
  ## The function returns the negative log-likelihood 
  - (x[1] * log(PC) + x[2] * log(PI) + x[3]* log(PT))
}

It is possible to use optim in R with just this implementation to compute the maximum-likelihood estimate of the allele parameters.

optim(c(0.3, 0.3), loglik, x = c(85, 196, 341))

## $par
## [1] 0.07085 0.18872
## 
## $value
## [1] 600.5
## 
## $counts
## function gradient 
##       71       NA 
## 
## $convergence
## [1] 0
## 
## $message
## NULL

The optim function uses an algorithm called Nelder-Mead as the default algorithm that relies on log-likelihood evaluations only. It is slow but fairly robust, though a bit of thought has to go into the initial parameter choice.

optim(c(0, 0), loglik, x = c(85, 196, 341))

## Error in optim(c(0, 0), loglik, x = c(85,
196, 341)): function cannot be evaluated at
initial parameters```

Starting the algorithm in a boundary value where the negative log-likelihood attains
the value $\infty$ does not work. 

The computations can beneficially be implemented in greater 
generality. The function `M` sums the cells that are collapsed, 
which has to be specified by the `group` argument.


```r
M <- function(x, group)
  as.vector(tapply(x, group, sum))

The log-likelihood is then implemented for multinomial cell collapsing via M and two problem specific arguments to the loglik function. One of these is a vector specifying the grouping structure of the collapsing. The other is a function that determines the parametrization that maps the parameter that we are optimizing over to the cell probabilities. In the implementation it is assumed that this prob function in addition encodes parameter constraints by returning NULL if parameter constraints are violated.

loglik <- function(par, x, prob, group, ...) {
  p <- prob(par)
  if(is.null(p)) return(Inf)
  - sum(x * log(M(prob(par), group)))
}

The function prob is implemented specifically for the peppered moths as follows.

prob <- function(p) {
  p[3] <- 1 - p[1] - p[2]
  if (p[1] > 1 || p[1] < 0 || p[2] > 1 || p[2] < 0 || p[3] < 0)
    return(NULL)
  c(p[1]^2, 2 * p[1] * p[2], 2* p[1] * p[3], 
    p[2]^2, 2 * p[2] * p[3], p[3]^2)
}

We test that the new implementation gives the same result when optimized as using the more problem specific implementation.

optim(c(0.3, 0.3), loglik, x = c(85, 196, 341), 
      prob = prob, group = c(1, 1, 1, 2, 2, 3))

## $par
## [1] 0.07085 0.18872
## 
## $value
## [1] 600.5
## 
## $counts
## function gradient 
##       71       NA 
## 
## $convergence
## [1] 0
## 
## $message
## NULL

Once we have found an estimate of the parameters, we can compute a prediction of the unobserved genotype counts from the phenotype counts using the conditional distribution of the genotypes given the phenotypes. This is straightforward as the conditional distribution of \(Y_{A_j} = (Y_k)_{k \in A_j}\), conditionally on \(X\) is also a multinomial distribution; \[Y_{A_j} \mid X = x \sim \textrm{Mult}\left( \frac{p_{A_j}}{M(p)_j}, x_j \right).\] The probability parameters are simply \(p\) restricted to \(A_j\) and renormalized to a probability vector. Observe that this gives \[E (Y_k \mid X = x) = \frac{x_j p_k}{M(p)_j}\] for \(k \in A_j\). Using the estimated parameters and the M function implemented above, we can compute a prediction of the genotype counts as follows.

x <- c(85, 196, 341)
group <- c(1, 1, 1, 2, 2, 3)
p <- prob(c(0.07084643, 0.18871900))
x[group] * p / M(p, group)[group]

## [1]   3.122  16.630  65.248  22.155 173.845 341.000

This is of interest in itself, but computing these conditional expectations will also be central for the EM algorithm in Chapter 8.

6.3 Regression models

Regression models are models of one variable, called the response, conditionally on one or more other variables, called the predictors. Typically we use models that assume conditional independence of the responses given the predictors, and a particularly convenient class of regression models is based on exponential families.

If we let \(y_i \in \mathbb{R}\) denote the \(i\)th response and \(x_i \in \mathbb{R}^p\) the \(i\)th predictor we can consider the exponential family of models with joint density \[f(\mathbf{y} \mid \mathbf{X}, \beta) = \prod_{i=1}^n e^{\theta^T t_i(y_i \mid x_i) - \log \varphi_i(\theta)}\] for suitably chosen base measures. Here \[\mathbf{X} = \left( \begin{array}{c} x_1^T \\ x_2^T \\ \vdots \\ x_{n-1}^T \\ x_n^T \end{array} \right)\] is called the model matrix and is an \(n \times p\) matrix.

Example 6.3 If \(y_i \in \mathbb{N}_0\) are counts we often use a Poisson regression model with point probabilities (density w.r.t. counting measure) \[p_i(y_i \mid x_i) = e^{-\mu(x_i)} \frac{\mu(x_i)^{y_i}}{y_i!}.\] If the mean depends on the predictors in a log-linear way, \(\log(\mu(x_i)) = x_i^T \beta\), then \[p_i(y_i \mid x_i) = e^{\beta^T x_i y_i - \exp( x_i^T \beta)} \frac{1}{y_i!}.\] The factor \(1/y_i!\) can be absorbed into the base measure, and we recognize this Poisson regression model as an exponential family with sufficient statistics \[t_i(y_i) = x_i y_i\] and \[\log \varphi_i(\beta) = \exp( x_i^T \beta).\]

To implement numerical optimization algorithms for computing the maximum-likelihood estimate we note that \[t(\mathbf{y}) = \sum_{i=1}^n x_i y_i = \mathbf{X}^T \mathbf{y} \quad \text{and} \quad \kappa(\beta) = \sum_{i=1}^n e^{x_i^T \beta},\] that \[\nabla \kappa(\beta) = \sum_{i=1}^n x_i e^{x_i^T \beta},\] and that \[D^2 \kappa(\beta) = \sum_{i=1}^n x_i x_i^T e^{x_i^T \beta} = \mathbf{X}^T \mathbf{W}(\beta) \mathbf{X}\] where \(\mathbf{W}(\beta)\) is a diagonal matrix with \(\mathbf{W}(\beta)_{ii} = \exp(x_i^T \beta).\) All these formulas follow directly from the general formulas for exponential families.

To illustrate the use of a Poisson regression model we consider the following data set from a major Swedish supermarket chain. It contains the number of bags of frozen vegetables sold in a given week in a given store under a marketing campaign. A predicted number of items sold in a normal week (without a campaign) based on historic sales is included. It is of interest to recalibrate this number to give a good prediction of the number of items actually sold.

vegetables <- read_csv("data/vegetables.csv", col_types = cols(store = "c"))

summary(vegetables)

##       sale         normalSale        store          
##  Min.   :  1.0   Min.   :  0.20   Length:1066       
##  1st Qu.: 12.0   1st Qu.:  4.20   Class :character  
##  Median : 21.0   Median :  7.25   Mode  :character  
##  Mean   : 40.3   Mean   : 11.72                     
##  3rd Qu.: 40.0   3rd Qu.: 12.25                     
##  Max.   :571.0   Max.   :102.00

It is natural to model the number of sold items using a Poisson regression model, and we will consider the following simple log-linear model:

\[\log(E(\text{sale} \mid \text{normalSale})) = \beta_0 + \beta_1 \log(\text{normalSale}).\]

This is an example of an exponential family regression model as above with a Poisson response distribution. It is a standard regression model that can be fitted to data using the glm function and using the formula interface to specify how the response should depend on the normal sale. The model is fitted by computing the maximum-likelihood estimate of the two parameters \(\beta_0\) and \(\beta_1\).

# A Poisson regression model
pois_model_null <- glm(
  sale ~ log(normalSale), 
  data = vegetables, 
  family = poisson
)  

summary(pois_model_null)

## 
## Call:
## glm(formula = sale ~ log(normalSale), family = poisson, data = vegetables)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -16.218   -2.677   -0.864    1.324   21.730  
## 
## Coefficients:
##                 Estimate Std. Error z value Pr(>|z|)
## (Intercept)        1.461      0.015    97.2   <2e-16
## log(normalSale)    0.922      0.005   184.4   <2e-16
##                    
## (Intercept)     ***
## log(normalSale) ***
## ---
## Signif. codes:  
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for poisson family taken to be 1)
## 
##     Null deviance: 51177  on 1065  degrees of freedom
## Residual deviance: 17502  on 1064  degrees of freedom
## AIC: 22823
## 
## Number of Fisher Scoring iterations: 5

The fitted model of the expected sale as a function of the normal sale, \(x\), is
\[x \mapsto e^{1.46 + 0.92 \times \log(x)} = (4.31 \times x^{-0.08}) \times x.\] This model roughly predicts a four-fold increase of the sale during a campaign, though the effect decays with increasing \(x\). If the normal sale is 10 items the factor is \(4.31 \times 10^{-0.08} = 3.58\), and if the normal sale is 100 items the factor reduces to \(4.31 \times 100^{-0.08} = 2.98\).

We are not entirely satisfied with this model. It is fitted across all stores in the data set, and it is not obvious that the same effect should apply across all stores. Thus we would like to fit a model of the form

\[\log(E(\text{sale})) = \beta_{\text{store}} + \beta_1 \log(\text{normalSale})\]

instead. Fortunately, this is also straightforward using glm.

## Note, variable store is a factor! The 'intercept' is removed 
## in the formula to obtain a parametrization as above. 
pois_model <- glm(
  sale ~ store + log(normalSale) - 1, 
  data = vegetables, 
  family = poisson
)

We will not print all the individual store effects as there are 352 individual stores.

summary(pois_model)$coefficients[c(1, 2, 3, 4, 353), ]

##                 Estimate Std. Error z value   Pr(>|z|)
## store1            2.7182    0.12756  21.309 9.416e-101
## store10           4.2954    0.12043  35.668 1.254e-278
## store100          3.4866    0.12426  28.060 3.055e-173
## store101          3.3007    0.11791  27.993 1.989e-172
## log(normalSale)   0.2025    0.03127   6.474  9.536e-11

We should note that the coefficient of \(\log(\text{normalSale})\) has changed considerably, and the model is a somewhat different model now for the individual stores.

From a computational viewpoint the most important thing that has changed is that the number of parameters has increased a lot. In the first and simple model there are two parameters. In the second model there are 353 parameters. Computing the maximum-likelihood estimate is a considerably more difficult problem in the second case.

6.4 Finite mixture models

A finite mixture model is a model of a pair of random variables \((Y, Z)\) with \(Z \in \{1, \ldots, K\}\), \(P(Z = k) = p_k\), and the conditional distribution of \(Y\) given \(Z = k\) having density \(f_k( \cdot \mid \theta_k)\). The joint density is then \[(y, k) \mapsto f_k(y \mid \theta_k) p_k,\] and the marginal density for the distribution of \(Y\) is \[f(y \mid \theta) = \sum_{k=1}^K f_k(y \mid \theta_k) p_k\] where \(\theta\) is the vector of all parameters. We say that the model has \(K\) mixture components and call \(f_k( \cdot \mid \theta_k)\) the mixture distributions and \(p_k\) the mixture weights.

The main usage of mixture models is to situations where \(Z\) is not observed. In practice, only \(Y\) is observed, and parameter estimation has to be based on the marginal distribution of \(Y\) with density \(f(\cdot \mid \theta)\), which is a weighted sum of the mixture distributions.

The set of all probability measures on \(\{1, \ldots, K\}\) is an exponential family with sufficient statistic \[\tilde{t}_0(k) = (\delta_{1k}, \delta_{2k}, \ldots, \delta_{(K-1)k}) \in \mathbb{R}^{K-1},\] canonical parameter \(\alpha = (\alpha_1, \ldots, \alpha_{K-1}) \in \mathbb{R}^{K-1}\) and \[p_k = \frac{e^{\alpha_k}}{1 + \sum_{l=1}^{K-1} e^{\alpha_l}}.\]

When \(f_k\) is an exponential family as well with sufficient statistic \(\tilde{t}_k : \mathcal{Y} \to \mathbb{R}^{p_k}\) and \(\theta_k\) the canonical parameter, we bundle \(\alpha, \theta_1, \ldots, \theta_K\) into \(\theta\) and define \[t_1(y) = \left(\begin{array}{c} \tilde{t}_0 \\ 0 \\ 0 \\ \vdots \\ 0 \end{array} \right)\] together with \[t_2(y \mid k) = \left(\begin{array}{c} 0 \\ \delta_{1k} \tilde{t}_1(y) \\ \delta_{2k} \tilde{t}_2(y) \\ \vdots \\ \delta_{Kk} \tilde{t}_K(y) \end{array} \right)\] we see that we have an exponential family of the joint distribution of \((Y, Z)\) with the \(p = K-1 + p_1 + \ldots + p_K\)-dimensional canonical parameter \(\theta\), with the sufficient statistic \(t_1\) determining the marginal distribution of \(Z\) and with the sufficient statistic \(t_2\) determining the conditional distribution of \(Y\) given \(Z\). We have here made the conditioning variable explicit.

The marginal density of \(Y\) in the exponential family parametrization then becomes \[f(y \mid \theta) = \sum_{k=1}^K e^{\theta^T (t_1(k) + t_2(y \mid k)) - \log \varphi_1(\theta) - \log \varphi_2(\theta \mid k)}.\] For small \(K\) it is usually unproblematic to implement the computation of the marginal density using the formula above, and the computation of derivatives can likewise be implemented based on the formulas derived in Section 6.1.3.

6.4.1 Gaussian mixtures

A Gaussian mixture model is a mixture model where all the mixture distributions are
Gaussian distributions but potentially with different means and variances. In this section we focus on the simplest Gaussian mixture model with \(K = 2\) mixture components.

When \(K = 2\), the Gaussian mixture model is parametrized by the five parameters: the mixture weight \(p = P(Z = 1) \in (0, 1)\), the two means \(\mu_1, \mu_2 \in \mathbb{R}\), and the two variances \(\sigma_1, \sigma_2 > 0\). This is not the parametrization using canonical exponential family parameters, which we return to below. First we will simply simulate random variables from this model.

sigma1 <- 1
sigma2 <- 2
mu1 <- -0.5
mu2 <- 4
p <- 0.5
n <- 5000
z <- sample(c(TRUE, FALSE), n, replace = TRUE, prob = c(p, 1 - p))
## Conditional simulation from the mixture components
y <- numeric(n)
n1 <- sum(z)
y[z] <- rnorm(n1, mu1, sigma1)
y[!z] <- rnorm(n - n1, mu2, sigma2)

The simulation above generated 5000 samples from a two-component Gaussian mixture model with mixture distributions \(\mathcal{N}(-0.5, 1)\) and \(\mathcal{N}(4, 4)\), and with each component having weight \(0.5\). This gives a bimodal distribution as illustrated by the histogram on Figure 6.1.

yy <- seq(-3, 11, 0.1)
dens <- p * dnorm(yy, mu1, sigma1) + (1 - p) * dnorm(yy, mu2, sigma2)
ggplot(mapping = aes(y, ..density..)) + 
  geom_histogram(bins = 20) + 
  geom_line(aes(yy, dens), color = "blue", size = 1) + 
  stat_density(bw = "SJ", geom="line", color = "red", size = 1)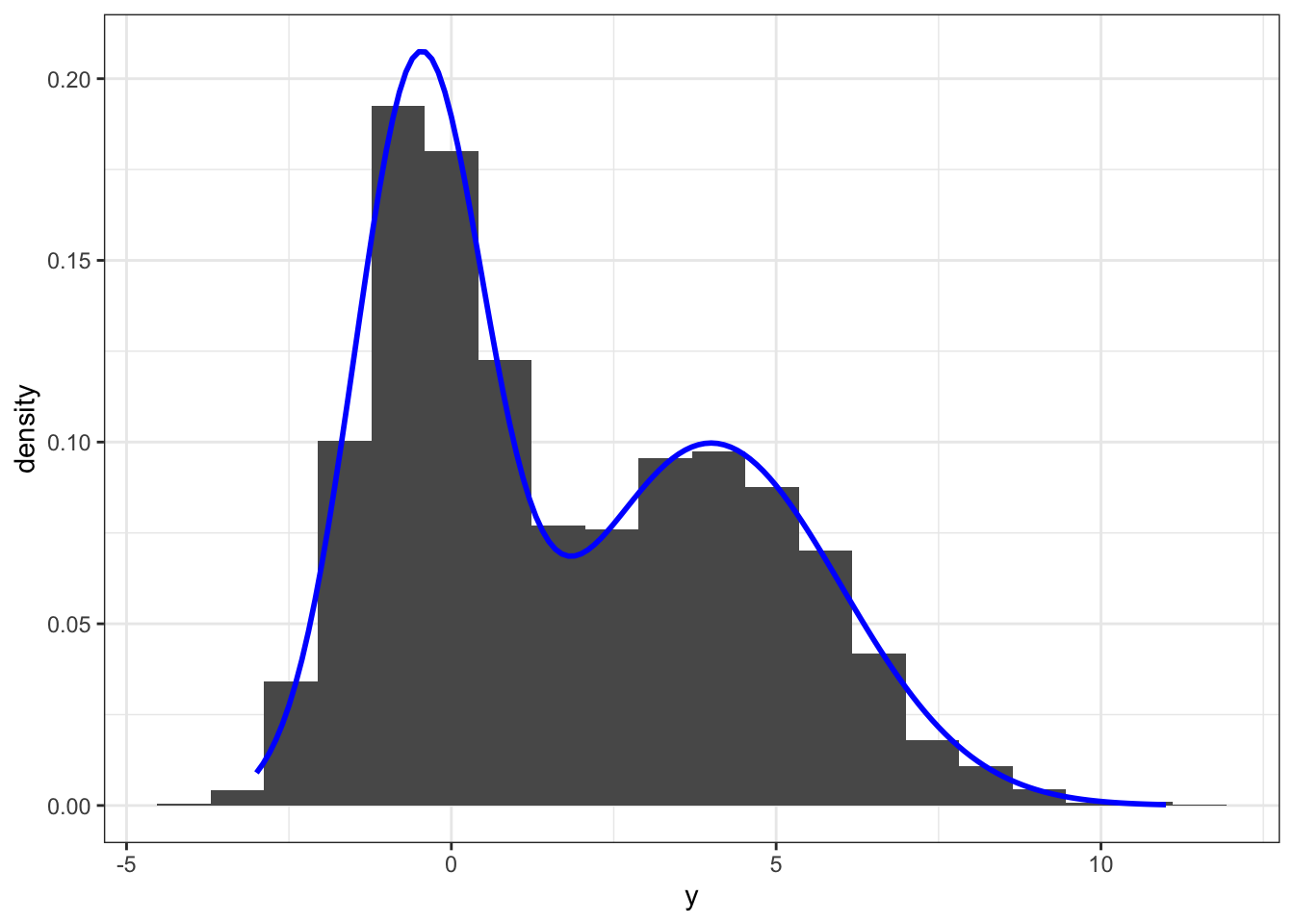

Figure 6.1: Histogram and density estimate (red) of data simulated from a two-component Gaussian mixture distribution. The true mixture distribution has

It is possible to give a mathematically different representation of the marginal distribution of \(Y\) that is sometimes useful. Though it gives the same marginal distribution from the same components, it does provide a different interpretation of what a mixture model is a model of, and it does provide a different way of simulating from a mixture distribution.

If we let \(Y_1 \sim \mathcal{N}(\mu_1, \sigma_1^2)\) and \(Y_2 \sim \mathcal{N}(\mu_2, \sigma_2^2)\) be independent, and independent of \(Z\), we can define

\[\begin{equation} Y = 1(Z = 1) Y_1 + 1(Z = 2) Y_2 = Y_{Z}. \tag{6.3} \end{equation}\]

Clearly, the conditional distribution of \(Y\) given \(Z = k\) is \(f_k\). From (6.3) it follows directly that \[E(Y^n) = P(Z = 1) E(Y_1^n) + P(Z = 2) E(Y_2^n) = p m_1(n) + (1 - p) m_2(n)\] where \(m_k(n)\) denotes the \(n\)th non-central moment of the \(k\)th mixture component. In particular,

\[E(Y) = p \mu_1 + (1 - p) \mu_2.\]

The variance can be found from the second moment as

\[\begin{align} V(Y) & = p(\mu_1^2 + \sigma_1^2) + (1-p)(\mu_2^2 + \sigma_2^2) - (p \mu_1 + (1 - p) \mu_2)^2 \\ & = p\sigma_1^2 + (1 - p) \sigma_2^2 + p(1-p)(\mu_1^2 + \mu_2^2 - 2 \mu_1 \mu_2). \end{align}\]

While it is certainly possible to derive this formula by other means, using (6.3) gives a simple argument based on elementary properties of expectation and independence of \((Y_1, Y_2)\) and \(Z\).

The construction via (6.3) has an interpretation that differs from how a mixture model was defined in the first place. Though \((Y, Z)\) has the correct joint distribution, \(Y\) is by (6.3) the result of \(Z\) selecting one out of two possible observations. The difference can best be illustrated by an example. Suppose that we have a large population consisting of married couples entirely. We can draw a sample of individuals (ignoring the marriage relations completely) from this population and let \(Z\) denote the sex and \(Y\) the height of the individual. Then \(Y\) follows a mixture distribution with two components corresponding to males and females according to the definition. At the risk of being heteronormative, suppose that all couples consist of one male and one female. We could then also draw a sample of married couples, and for each couple flip a coin to decide whether to report the male’s or the female’s height. This corresponds to the construction of \(Y\) by (6.3). We get the same marginal mixture distribution of heights though.

Arguably the heights of individuals in a marriage are not independent, but this is actually immaterial. Any dependence structure between \(Y_1\) and \(Y_2\) is lost in the transformation (6.3), and we can just as well assume them independent for mathematical convenience. We won’t be able to tell the difference from observing only \(Y\) (and \(Z\)) anyway.

We illustrate below how (6.3) can be used for alternative implementations of ways to simulate from the mixture model. We compare empirical means and variances to the theoretical values to test if all the implementations actually simulate from the Gaussian mixture model.

## Mean
mu <- p * mu1 + (1 - p) * mu2

## Variance 
sigmasq <- p * sigma1^2 + (1 - p) * sigma2^2 + 
  p * (1-p)*(mu1^2 + mu2^2 - 2 * mu1 * mu2)

## Simulation using the selection formulation via 'ifelse'
y2 <- ifelse(z, rnorm(n, mu1, sigma1), rnorm(n, mu2, sigma2))

## Yet another way of simulating from a mixture model
## using arithmetic instead of 'ifelse' for the selection 
## and with Y_1 and Y_2 actually being dependent
y3 <- rnorm(n)
y3 <- z * (sigma1 * y3 + mu1) + (!z) * (sigma2 * y3 + mu2)

## Returning to the definition again, this last method simulates conditionally 
## from the mixture components via transformation of an underlying Gaussian
## variable with mean 0 and variance 1
y4 <- rnorm(n)
y4[z] <- sigma1 * y4[z] + mu1
y4[!z] <- sigma2 * y4[!z] + mu2

## Tests
data.frame(mean = c(mu, mean(y), mean(y2), mean(y3), mean(y4)),
      variance = c(sigmasq, var(y), var(y2), var(y3), var(y4)), 
      row.names = c("true", "conditional", "ifelse", "arithmetic", 
                    "conditional2" ))

##               mean variance
## true         1.750    7.562
## conditional  1.728    7.382
## ifelse       1.713    7.514
## arithmetic   1.708    7.566
## conditional2 1.700    7.464

In terms of run time there is not a big difference between three of the ways of simulating from a mixture model. A benchmark study (not shown) will reveal that the first and third methods are comparable in terms of run time and slightly faster than the fourth, while the second using ifelse takes more than twice as much time as the others. This is unsurprising as the ifelse method takes (6.3) very literally and generates twice the number of Gaussian variables actually needed.

The marginal density of \(Y\) is \[f(y) = p \frac{1}{\sqrt{2 \pi \sigma_1^2}} e^{-\frac{(y - \mu_1)^2}{2 \sigma_1^2}} + (1 - p)\frac{1}{\sqrt{2 \pi \sigma_2^2}}e^{-\frac{(y - \mu_2)^2}{2 \sigma_2^2}}\] as given in terms of the parameters \(p\), \(\mu_1, \mu_2\), \(\sigma_1^2\) and \(\sigma_2^2\).

Returning to the canonical parameters we see that they are given as follows: \[\theta_1 = \log \frac{p}{1 - p}, \quad \theta_2 = \frac{\mu_1}{2\sigma_1^2}, \quad \theta_3 = \frac{1}{2\sigma_1^2}, \quad \theta_4 = \frac{\mu_2}{\sigma_2^2}, \quad \theta_5 = \frac{1}{2\sigma_2^2}.\]

The joint density in this parametrization then becomes \[(y,k) \mapsto \left\{ \begin{array}{ll} \exp\left(\theta_1 + \theta_2 y - \theta_3 y^2 - \log (1 + e^{\theta_1}) - \frac{ \theta_2^2}{4\theta_3}+ \frac{1}{2} \log(\theta_3) \right) & \quad \text{if } k = 1 \\ \exp\left(\theta_4 y - \theta_5 y^2 - \log (1 + e^{\theta_1}) - \frac{\theta_4^2}{4\theta_5} + \frac{1}{2}\log(\theta_5) \right) & \quad \text{if } k = 2 \end{array} \right. \] and the marginal density for \(Y\) is

\[\begin{align} f(y \mid \theta) & = \exp\left(\theta_1 + \theta_2 y - \theta_3 y^2 - \log (1 + e^{\theta_1}) - \frac{ \theta_2^2}{4\theta_3}+ \frac{1}{2} \log(\theta_3) \right) \\ & + \exp\left(\theta_4 y - \theta_5 y^2 - \log (1 + e^{\theta_1}) - \frac{\theta_4^2}{4\theta_5} + \frac{1}{2}\log(\theta_5) \right). \end{align}\]

There is no apparent benefit to the canonical parametrization when considering the marginal density. It is, however, of value when we need the logarithm of the joint density as we will for the EM-algorithm.

6.5 Mixed models

A mixed model is a regression model of observations that allows for random variation at two different levels. In this section we will focus on mixed models in an exponential family context. Mixed models can be considered in greater generality but there will then be little shared structure and one has to deal with the models much more on a case-by-case manner.

In a mixed model we have observations \(y_j \in \mathcal{Y}\) and \(z \in \mathcal{Z}\) such that:

• the distribution of \(z\) is an exponential family with canonical parameter \(\theta_0\)
• conditionally on \(z\) the \(y_j\)s are independent with a distribution from an exponential family with sufficient statistics \(t_j( \cdot \mid z)\).

This definition emphasizes how the \(y_j\)s have variation at two levels. There is variation in the underlying \(z\), which is the first level of variation (often called the random effect), and then there is variation among the \(y_j\)s given the \(z\), which is the second level of variation. It is a special case of hierarchical models (Bayesian networks with tree graphs) also known as multilevel models, with the mixed model having only two levels. When we observe data from such a model we typically observe independent replications, \((y_{ij})_{j=1, \ldots, m_i}\) for \(i = 1, \ldots, n\), of the \(y_j\)s only. Note that we allow for a different number, \(m_i\), of \(y_j\)s for each \(i\).

The simplest class of mixed models is obtained by \(t_j = t\) not depending on \(j\), and \[t(y_j \mid z) = \left(\begin{array}{cc} t_1(y_j) \\ t_2(y_j, z) \end{array} \right)\] for some fixed maps \(t_1 : \mathcal{Y} \mapsto \mathbb{R}^{p_1}\) and \(t_2 : \mathcal{Y} \times \mathcal{Z} \mapsto \mathbb{R}^{p_2}\). This is called a random effects model (this is a model where there are no fixed effects in the sense that \(t_j\) does not depend on \(j\), and given the random effect \(z\) the \(y_j\)s are i.i.d.). The canonical parameters associated with such a model are \(\theta_0\) that enters into the distribution of the random effect, \(\theta_1 \in \mathbb{R}^{p_1}\) and \(\theta_2 \in \mathbb{R}^{p_2}\) that enter into the conditional distribution of \(y_j\) given \(z\).

Example 6.4 The special case of a Gaussian, linear random effects model is the model where \(z\) is \(\mathcal{N}(0, 1)\) distributed, \(\mathcal{Y} = \mathbb{R}\) (with base measure proportional to Lebesgue measure) and the sufficient statistic is \[t(y_j \mid z) = \left(\begin{array}{cc} y_j \\ - y_j^2 \\ zy_j \end{array}\right).\] There are no free parameters in the distribution of \(z\).

From Example 6.2 it follows that the conditional variance of \(y\) given \(z\) is \[\sigma^2 = \frac{1}{2\theta_2}\] and the conditional mean of \(y\) given \(z\) is \[\frac{\theta_1 + \theta_3 z}{2 \theta_2} = \sigma^2 \theta_1 + \sigma^2 \theta_3 z.\] Reparametrizing in terms of \(\sigma^2\), \(\beta_0 = \sigma^2 \theta_1\) and \(\nu = \sigma^2 \theta_3\) we see how the conditional distribution of \(y_j\) given \(z\) is \(\mathcal{N}(\beta_0 + \nu z, \sigma^2)\). From this it is clear how the mixed model of \(y_j\) conditionally on \(z\) is a regression model. However, we do not observe \(z\) in practice.

Using the above distributional result we can see that the Gaussian random effects model of observations \(y_{ij}\) can equivalently be stated as

\[Y_{ij} = \beta_0 + \nu Z_i + \varepsilon_{ij}\]

for \(i = 1, \ldots, n\) and \(j = 1, \ldots, m_i\) where \(Z_1, \ldots, Z_n\) are i.i.d. \(\mathcal{N}(0, 1)\)-distributed and independent of \(\varepsilon_{11}, \varepsilon_{12}, \ldots, \varepsilon_{1n_1}, \ldots, \varepsilon_{mn_m}\) that are themselves i.i.d. \(\mathcal{N}(0, \sigma^2)\)-distributed.