4 Univariate random variables
This chapter will deal with algorithms for simulating observations from a distribution on \(\mathbb{R}\) or any subset thereof. There can be several purposes of doing so, for instance:
- We want to investigate properties of the distribution.
- We want to simulate independent realizations of univariate random variables to investigate the distribution of a transformation.
- We want to use Monte Carlo integration to compute numerically an integral (which could be a probability).
In this chapter the focus is on the simulation of a single random variable or an i.i.d. sequence of random variables primarily via various transformations of pseudorandom numbers. The pseudo random numbers themselves being approximate simulations of i.i.d. random variables uniformly distributed on \((0, 1)\).
4.1 Pseudorandom number generators
Most simulation algorithms are based on algorithms for generating pseudorandom uniformly distributed variables in \((0, 1)\). They arise from deterministic integer sequences initiated by a seed. A classical example of a pseudorandom integer generator is the linear congruential generator. A sequence of numbers from this generator is computed iteratively by \[x_{n+1} = (a x_n + c) \text{ mod m}\] for integer parameters \(a\), \(c\) and \(m\). The seed \(x_1\) is a number between \(0\) and \(m - 1\), and the resulting sequence is in the set \(\{0, \ldots, m - 1\}\). The ANSI C standard specifies the choices \(m = 2^{31}\), \(a = 1,103,515,245\) and \(c = 12,345\). The generator is simple to understand and implement but has been superseded by much better generators.
Pseudorandom number generators are generally defined in terms of a finite state space \(\mathcal{Z}\) and a one-to-one map \(f : \mathcal{Z} \to \mathcal{Z}\). The generator produces a sequence in \(\mathcal{Z}\) iteratively from the seed \(\mathbf{z}_1 \in \mathcal{Z}\) by \[\mathbf{z}_n = f(\mathbf{z}_{n-1}).\] Pseudorandom integers are typically obtained as \[x_n = h(\mathbf{z}_n)\] for a transformation \(h : \mathcal{Z} \mapsto \mathbb{Z}\). If the image of \(h\) is in the set \(\{0, 1, \ldots, 2^{w} - 1\}\) of \(w\)-bit integers, pseudorandom numbers in \([0, 1)\) are typically obtained as \[x_n = 2^{-w} h(\mathbf{z}_n).\]
In R, the default pseudorandom number generator is the 32-bit Mersenne Twister, which generates integers in the range \[\{0, 1, \ldots, 2^{32} -1\}.\] The state space is \[\mathcal{Z} = \{0, 1, \ldots, 2^{32} -1\}^{624},\] that is, a state is a 624 dimensional vector of 32-bit integers. The function \(f\) is of the form \[f(\mathbf{z}) = (z_2, z_3, \ldots, z_{623}, f_{624}(z_1, z_2, z_{m + 1})),\] for \(1 \leq m < 624\), and \(h\) is a function of \(z_{624}\) only. The standard choice \(m = 397\) is used in the R implementation. The function \(f_{624}\) is a bit complicated, it includes what is known as the twist transformation, and it requires additional parameters. The period of the generator is the astronomical number \[2^{32 \times 624 - 31} - 1 = 2^{19937} - 1,\] which is a Mersenne prime. Moreover, all combinations of consecutive integers up to dimension 623 occur equally often in a period, and empirical tests of the generator demonstrate that it has good statistical properties, though it is known to fail some tests.
In R you can set the seed using the function set.seed that takes an
integer argument and produces an element in the state space. The argument
given to set.seed is not the actual seed, and set.seed computes a
valid seed for any pseudorandom number generator that R is using,
whether it is the Mersenne Twister or not. Thus the use of set.seed is
the safe and recommended way of setting a seed.
The actual seed (together with some additional information) can be accessed
via the vector .Random.seed. Its first entry, .Random.seed[1], encodes the
pseudorandom number generator used as well as the generator for
Gaussian variables and discrete uniform variables. This
information is decoded by RNGkind().
RNGkind()## [1] "Mersenne-Twister" "Inversion" "Rejection"For the Mersenne Twister,
.Random.seed[3:626] contains the vector in the state space, while
.Random.seed[2] contains the “current position” in the state vector.
The implementation needs a position variable because it does 624 updates of the
state vector at a time and then runs through those values sequentially
before the next update. This is equivalent to but more efficient than e.g.
implementing the position shifts explicitly as in the definition of \(f\) above.
set.seed(27112015) ## Computes a new seed from an integer
oldseed <- .Random.seed[-1] ## The actual seed
.Random.seed[1] ## Encoding of generators used, will stay fixed## [1] 10403
.Random.seed[2] ## Start position after the seed has been set is 624## [1] 624
tmp <- runif(1)
tmp## [1] 0.7793Every time a random number is generated, e.g. by runif above, the same underlying
sequence of pseudorandom numbers is used, and the state vector stored in
.Random.seed is updated accordingly.
head(oldseed, 5)## [1] 624 -1660633125 -1167670944 1031453153 815285806
head(.Random.seed[-1], 5) ## The state vector and position has been updated## [1] 1 -696993996 -1035426662 -378189083 -745352065## [1] 0.7793 0.5613
head(.Random.seed[-1], 5) ## The state vector has not changed, only the position## [1] 2 -696993996 -1035426662 -378189083 -745352065Resetting the seed will restart the pseudorandom number generator with the same seed and result in the same sequence of random numbers.
## [1] 624 -1660633125 -1167670944 1031453153 815285806
head(oldseed, 5) ## Same as current .Random.seed## [1] 624 -1660633125 -1167670944 1031453153 815285806
runif(1) ## Same as tmp## [1] 0.7793Note that when using any of the standard R generators, any value of \(0\) or \(1\) returned by the underlying pseudorandom uniform generator is adjusted to be in \((0,1)\). Thus uniform random variables are guaranteed to be in \((0, 1)\).
Some of the random number generators implemented in R use more than one pseudorandom number per variable. This is, for instance, the case when we simulate Gamma distributed random variables.
## [1] 1.193
head(.Random.seed[-1], 5) ## Position changed to 2## [1] 2 -696993996 -1035426662 -378189083 -745352065
rgamma(1, 1) ## A single Gamma distributed random number## [1] 0.2795
head(.Random.seed[-1], 5) ## Position changed to 5## [1] 5 -696993996 -1035426662 -378189083 -745352065In the example above, the first Gamma variable required two pseudorandom numbers, while the second required three pseudorandom numbers. The detailed explanation is given in Section 4.3, where it is shown how to generate random variables from the Gamma distribution via rejection sampling. This requires as a minimum two pseudorandom numbers for every Gamma variable generated.
4.1.1 Implementing a pseudorandom number generator
The development of high quality pseudorandom number generators is a research field in itself. This is particularly true if one needs theoretical guarantees for randomized algorithms or cryptographically secure generators. For scientific computations and simulations correct statistical properties, reproducibility and speed are more important than cryptographic security, but even so, it is not trivial to invent a good generator, and the field is still developing. For a generator to be seriously considered, its mathematical properties should be well understood, and it should pass (most) tests in standardized test suites such as TestU01, see L’Ecuyer and Simard (2007).
R provides a couple of alternatives to the Mersenne Twister,
see ?RNG, but there is no compelling reason to switch to any of those for ordinary
use. They are mostly available for historical reasons.
One exception is the L’Ecuyer-CMRG generator, which is useful when
independent pseudorandom sequences are needed for parallel computations.
Though the Mersenne Twister is a widely used pseudorandom number generator, it has well known shortcomings. There are high quality alternatives that are simpler and faster, such as the family of shift-register generators and their variations, but they are not currently available from the base R package.
Shift-register generators are based on linear transformations of the bit representation of integers. Three particular transformations are typically composed; the \(\mathrm{Lshift}\) and \(\mathrm{Rshift}\) operators and the bitwise \(\mathrm{xor}\) operator. Let \(z = [z_{31}, z_{30}, \ldots, z_0]\) with \(z_i \in \{0, 1\}\) denote the bit representation of a 32-bit (unsigned) integer \(z\) (ordered from most significant bit to least significant bit). That is, \[z = z_{31} 2^{31} + z_{30} 2^{30} + \ldots + z_2 2^2 + z_1 2^{1} + z_0.\] Then the left shift operator is defined as \[\mathrm{Lshift}(z) = [z_{30}, z_{29}, \ldots, z_0, 0],\] and the right shift operator is defined as \[\mathrm{Rshift}(z) = [0, z_{31}, z_{30}, \ldots, z_1].\] The bitwise xor operator is defined as \[\mathrm{xor}(z, z') = [\mathrm{xor}(z_{31},z_{31}') , \mathrm{xor}(z_{30}, z_{30}'), \ldots, \mathrm{xor}(z_0, z_0')]\] where \(\mathrm{xor}(0, 0) = \mathrm{xor}(1, 1) = 0\) and \(\mathrm{xor}(1, 0) = \mathrm{xor}(0, 1) = 1\). Thus a transformation could be of the form \[\mathrm{xor}(z, \mathrm{Rshift}^2(z)) = [\mathrm{xor}(z_{31}, 0) , \mathrm{xor}(z_{30}, 0), \mathrm{xor}(z_{29}, z_{31}), \ldots, \mathrm{xor}(z_0, z_2)].\]
One example of a shift-register based generator is Marsaglia’s xorwow algorithm, Marsaglia (2003). In addition to the shift and xor operations, the output of this generator is perturbed by a sequence of integers with period \(2^{32}\). The state space of the generator is \[\{0, 1, \ldots, 2^{32} -1\}^{5}\] with \[f(\mathbf{z}) = (z_1 + 362437 \ (\mathrm{mod}\ 2^{32}), f_1(z_5, z_2), z_2, z_3, z_4),\] and \[h(\mathbf{z}) = 2^{-32} (z_1 + z_2).\] The number 362437 is Marsaglia’s choice for generating what he calls a Weyl sequence, but any odd number will do. The function \(f_1\) is given as \[f_1(z, z') = \mathrm{xor}(\mathrm{xor}(z, \mathrm{Rshift}^2(z)), \mathrm{xor}(z', \mathrm{xor}(\mathrm{Lshift}^4(z'), \mathrm{Lshift}(\mathrm{xor}(z, \mathrm{Rshift}^2(z)))))).\]
This may look intimidating, but all the operations are very elementary. Take the number \(z = 123456\), say, then the intermediate value \(\overline{z} = \mathrm{xor}(z, \mathrm{Rshift}^2(z))\) is computed as follows:
\[ \begin{array}{ll} z & \texttt{00000000 00000001 11100010 01000000} \\ \mathrm{Rshift}^2(z) & \texttt{00000000 00000000 01111000 10010000} \\ \hline \mathrm{xor} & \texttt{00000000 00000001 10011010 11010000} \end{array} \]
And if \(z' = 87654321\) the value of \(f_1(z, z')\) is computed like this:
\[ \begin{array}{ll} \mathrm{Lshift}^4(z') & \texttt{01010011 10010111 11111011 00010000} \\ \mathrm{Lshift}(\overline{z}) & \texttt{00000000 00000011 00110101 10100000} \\ \hline \mathrm{xor} & \texttt{01010011 10010100 11001110 10110000} \\ z' & \texttt{00000101 00111001 01111111 10110001} \\ \hline \mathrm{xor} & \texttt{01010110 10101101 10110001 00000001} \\ \overline{z} & \texttt{00000000 00000001 10011010 11010000} \\ \hline \mathrm{xor} & \texttt{01010110 10101100 00101011 11010001} \end{array} \]
Converted back to a 32-bit integer, the result is \(f_1(z, z') = 1454123985\). The shift and xor operations are tedious to do by hand but extremely fast on modern computer architectures, and shift-register based generators are some of the fastest generators with good statistical properties.
To make R use the xorwow generator we need to implement it as a user supplied
generator. This requires writing the C code that implements the generator,
compiling the code into a shared object file, loading it into
R with the dyn.load function, and finally calling RNGkind("user")
to make R use this pseudorandom number generator. See ?Random.user
for some details and an example.
Using the Rcpp package, and sourceCpp, in particular, is usually much preferred
over manual compiling and loading. However, in this case we need to make
functions available to the internals of R rather than exporting functions to be
callable from the R console. That is, nothing needs to be exported from C/C++.
If nothing is exported, sourceCpp will actually not load the shared object
file, so we need to trick sourceCpp to do so anyway. In the implementation
below we achieve this by simply exporting a direct interface to the xorwow generator.
#include <Rcpp.h>
#include <R_ext/Random.h>
/* The Random.h header file contains the function declarations for the functions
that R rely on internally for a user defined generator, and it also defines
the type Int32 as an unsigned int. */
static Int32 z[5]; // The state vector
static double res;
static int nseed = 5; // Length of the state vector
// Implementation of xorwow from Marsaglia's "Xorshift RNGs"
// modified so as to return a double in [0, 1). The '>>' and '<<'
// operators in C are bitwise right and left shift operators, and
// the caret, '^', is the xor operator.
double * user_unif_rand()
{
Int32 t = z[4];
Int32 s = z[1];
z[0] += 362437;
z[4] = z[3];
z[3] = z[2];
z[2] = s;
// Right shift t by 2, then bitwise xor between t and its shift
t ^= t >> 2;
// Left shift t by 1 and s by 4, xor them, xor with s and xor with t
t ^= s ^ (s << 4) ^ (t << 1);
z[1] = t;
res = (z[0] + t) * 2.32830643653869e-10;
return &res;
}
// A seed initializer using Marsaglia's congruential PRNG
void user_unif_init(Int32 seed_in) {
z[0] = seed_in;
z[1] = 69069 * z[0] + 1;
z[2] = 69069 * z[1] + 1;
z[3] = 69069 * z[2] + 1;
z[4] = 69069 * z[3] + 1;
}
// Two functions to make '.Random.seed' in R reflect the state vector
int * user_unif_nseed() { return &nseed; }
int * user_unif_seedloc() { return (int *) &z; }
// Wrapper to make 'user_unif_rand' callable from R
double xor_runif() {
return *user_unif_rand();
}
// This module will export two functions to be directly available from R.
// Note: if nothing is exported, `sourceCpp` will not load the shared
// object file generated by the compilation of the code, and
// 'user_unif_rand' will not become available to the internals of R.
RCPP_MODULE(xorwow) {
Rcpp::function("xor_set.seed", &user_unif_init, "Seeds Marsaglia's xorwow");
Rcpp::function("xor_runif", &xor_runif, "A uniform from Marsaglia's xorwow");
}We first test the direct interface to the xorwow algorithm.
xor_set.seed(3573076633)
xor_runif()## [1] 0.9091Then we set R’s pseudorandom number generator to be our user supplied generator.
default_prng <- RNGkind("user")All R’s standard random number generators will after the call RNGkind("user")
rely on the user provided generator, in this case the xorwow generator.
Note that R does an “initial scrambling” of the argument given to set.seed
before it is passed on to our user defined initializer. This
scrambling turns 24102019 used below into 3573076633 used above.
set.seed(24102019)
.Random.seed[-1] ## The state vector as seeded ## [1] -721890663 9136518 -310030769 1191753796 194708085
runif(1) ## As above since same unscrambled seed is used## [1] 0.9091
.Random.seed[-1] ## The state vector after one update## [1] -721528226 331069150 9136518 -310030769 1191753796The code above shows the state vector of the xorwow algorithm when seeded
by the user_unif_init function, and it also shows the
update to the state vector after a single iteration of the xorwow algorithm.
Though the xorwow algorithm is fast and simple, a benchmark study (not shown)
reveals that using xorwow instead of the Mersenne Twister doesn’t impact the
run time in a notable way when using e.g. runif. The generator is simply
not the bottleneck. As the implementation
of xorwow above is experimental and has not been thoroughly tested, we will
not rely on it and quickly reset the random number generator to its default value.
## Resetting the generator to the default
RNGkind(default_prng[1])4.1.2 Pseudorandom number packages
To benefit from the recent developments in pseudorandom number generators
we can turn to R packages such as the dqrng
package. It implements pcg64 from the PCG family of
generators as well as Xoroshiro128+ and Xoshiro256+
that are shift-register algorithms. Xoroshiro128+ is the default and other
generators can be chosen using dqRNGkind. The usage of generators from dqrng
is similar to the usage of base R generators.
library(dqrng)
dqset.seed(24102019)
dqrunif(1)## [1] 0.6172Using the generators from dqrng does not interfere with the base R generators as the state vectors are completely separated.
In addition to uniform pseudorandom variables generated by dqrunif the
dqrng package can generate exponential (dqrexp) and Gaussian (dqrnorm)
random variables as well as uniform discrete distributions (dqsample and
dqsample.int). All based on the fast pseudorandom integer generators that
the package includes. In addition, the package has a C++ interface that makes it
possible to use its generators in compiled code as well.
## # A tibble: 2 × 6
## expression min median `itr/sec` mem_alloc `gc/sec`
## <bch:expr> <bch:tm> <bch:tm> <dbl> <bch:byt> <dbl>
## 1 runif(1e+06) 4.74ms 5.43ms 183. 7.63MB 6.68
## 2 dqrunif(1e+06) 2.86ms 3.51ms 280. 7.63MB 8.95As the benchmark above shows, dqrunif is about six times faster than
runif when generating one million variables. The other generators provided
by the dqrng package show similar improvements over the base R generators.
4.2 Transformation techniques
If \(T : \mathcal{Z} \to \mathbb{R}\) is a map and \(Z \in \mathcal{Z}\) is a random variable we can simulate, then we can simulate \(X = T(Z).\)
Theorem 4.1 If \(F^{\leftarrow} : (0,1) \mapsto \mathbb{R}\) is the (generalized) inverse of a distribution function and \(U\) is uniformly distributed on \((0, 1)\) then the distribution of \[F^{\leftarrow}(U)\] has distribution function \(F\).
The proof of Theorem 4.1 can be found in many textbooks and will be skipped. It is easiest to use this theorem if we have an analytic formula for the inverse distribution function. But even in cases where we don’t it might be useful for simulation anyway if we have a very accurate approximation that is fast to evaluate.
The call RNGkind() in the previous section revealed that the default in R for generating samples from \(\mathcal{N}(0,1)\) is inversion. That is,
Theorem 4.1 is used to transform
uniform random variables with the inverse distribution function \(\Phi^{-1}\).
This function is, however, non-standard, and R implements a
technical approximation of \(\Phi^{-1}\) via rational functions.
4.2.1 Sampling from a \(t\)-distribution
Let \(Z = (Y, W) \in \mathbb{R} \times (0, \infty)\) with \(Z \sim \mathcal{N}(0, 1)\) and \(W \sim \chi^2_k\) independent.
Define \(T : \mathbb{R} \times (0, \infty) \to \mathbb{R}\) by \[T(z,w) = \frac{z}{\sqrt{w/k}},\] then \[X = T(Z, W) = \frac{Z}{\sqrt{W/k}} \sim t_k.\]
This is how R simulates from a \(t\)-distribution with \(W\) generated from a gamma distribution with shape parameter \(k / 2\) and scale parameter \(2\).
4.3 Rejection sampling
This section deals with a general algorithm for simulating variables from a distribution with density \(f\). We call \(f\) the target density and the corresponding distribution is called the target distribution. The idea is to simulate proposals from a different distribution with density \(g\) (the proposal distribution) and then according to a criterion decide to accept or reject the proposals. It is assumed throughout that the proposal density \(g\) is a density fulfilling that
\[\begin{equation} g(x) = 0 \Rightarrow f(x) = 0. \tag{4.1} \end{equation}\]
Let \(Y_1, Y_2, \ldots\) be i.i.d. with density \(g\) on \(\mathbb{R}\) and \(U_1, U_2, \ldots\) be i.i.d. uniformly distributed on \((0,1)\) and independent of the \(Y_i\)-s. Define \[T(\mathbf{Y}, \mathbf{U}) = Y_{\sigma}\] with \[\sigma = \inf\{n \geq 1 \mid U_n \leq \alpha f(Y_n) / g(Y_n)\},\] for \(\alpha \in (0, 1]\) and \(f\) a density. Rejection sampling then consists of simulating independent pairs \((Y_n, U_n)\) as long as we reject the proposals \(Y_n\) sampled from \(g\), that is, as long as \[U_n > \alpha f(Y_n) / g(Y_n).\] The first time we accept a proposal is \(\sigma\), and then we stop the sampling and return the proposal \(Y_{\sigma}\). The result is, indeed, a sample from the distribution with density \(f\) as the following theorem states.
Theorem 4.2 If \(\alpha f(y) \leq g(y)\) for all \(y \in \mathbb{R}\) and \(\alpha > 0\) then the distribution of \(Y_{\sigma}\) has density \(f\).
Proof. Note that \(g\) automatically fulfills (4.1). The formal proof decomposes the event \((Y_{\sigma} \leq y)\) according to the value of \(\sigma\) as follows
\[\begin{align} P(Y_{\sigma} \leq y) & = \sum_{n = 1}^{\infty} P(Y_{n} \leq y, \ \sigma = n) \\ & = \sum_{n = 1}^{\infty} P(Y_{n} \leq y, \ U_n \leq \alpha f(Y_n) / g(Y_n)) P(\sigma > n - 1) \\ & = P(Y_{1} \leq y, \ U_1 \leq \alpha f(Y_1) / g(Y_1)) \sum_{n = 1}^{\infty} P(\sigma > n - 1). \end{align}\]
By independence of the pairs \((Y_n, U_n)\) we find that \[P(\sigma > n - 1) = p^{(n-1)}\] where \(p = P(U_1 > \alpha f(Y_1) / g(Y_1))\), and \[\sum_{n = 1}^{\infty} P(\sigma > n - 1) = \sum_{n = 1}^{\infty} p^{(n-1)} = \frac{1}{1 - p}.\]
We further find using Tonelli’s theorem that
\[\begin{align} P(Y_{1} \leq y, \ U_1 \leq \alpha f(Y_1) / g(Y_1)) & = \int_{-\infty}^y \alpha \frac{f(z)}{g(z)} g(z) \mathrm{d}z \\ & = \alpha \int_{-\infty}^y f(z) \mathrm{d} z. \end{align}\]
It also follows from this, by taking \(y = \infty\), that \(1 - p = \alpha\), and we conclude that \[P(Y_{\sigma} \leq y) = \int_{-\infty}^y f(z) \mathrm{d} z,\] and the density for the distribution of \(Y_{\sigma}\) is, indeed, \(f\).
Note that if \(\alpha f \leq g\) for densities \(f\) and \(g\), then \[\alpha = \int \alpha f(x) \mathrm{d}x \leq \int g(x) \mathrm{d}x = 1,\] whence it follows automatically that \(\alpha \leq 1\) whenever \(\alpha f\) is dominated by \(g\). The function \(g/\alpha\) is called the envelope of \(f\). The tighter the envelope, the smaller is the probability of rejecting a sample from \(g\), and this is quantified explicitly by \(\alpha\) as \(1 - \alpha\) is the rejection probability. Thus \(\alpha\) should preferably be as close to one as possible.
If \(f(y) = c q(y)\) and \(g(y) = d p(y)\) for (unknown) normalizing constants \(c, d > 0\) and \(\alpha' q \leq p\) for \(\alpha' > 0\) then \[\underbrace{\left(\frac{\alpha' d}{c}\right)}_{= \alpha} \ f \leq g.\] The constant \(\alpha'\) may be larger than 1, but from the argument above we know that \(\alpha \leq 1\), and Theorem 4.2 gives that \(Y_{\sigma}\) has distribution with density \(f\). It appears that we need to compute the normalizing constants to implement rejection sampling. However, observe that \[u \leq \frac{\alpha f(y)}{g(y)} \Leftrightarrow u \leq \frac{\alpha' q(y)}{p(y)},\] whence rejection sampling can actually be implemented with knowledge of the unnormalized densities and \(\alpha'\) only and without computing \(c\) or \(d\). This is one great advantage of rejection sampling. We should note, though, that when we don’t know the normalizing constants, \(\alpha'\) does not tell us anything about how tight the envelope is, and thus how small the rejection probability is.
Given two functions \(q\) and \(p\), how do we then find \(\alpha'\) so that \(\alpha' q \leq p\)? Consider the function \[y \mapsto \frac{p(y)}{q(y)}\] for \(q(y) > 0\). If this function is lower bounded by a value strictly larger than zero, we can take \[\alpha' = \inf_{y: q(y) > 0} \frac{p(y)}{q(y)} > 0.\] We can in practice often find this value by minimizing \(p(y)/q(y)\). If the minimum is zero, there is no \(\alpha'\), and \(p\) cannot be used to construct an envelope. If the minimum is strictly positive it is the best possible choice of \(\alpha'\).
4.3.1 von Mises distribution
Recall the von Mises distribution from Section 1.2.1. It is a distribution on \((-\pi, \pi]\) with density \[f(x) \propto e^{\kappa \cos(x - \mu)}\] for parameters \(\kappa > 0\) and \(\mu \in (-\pi, \pi]\). Clearly, \(\mu\) is a location parameter, and we fix \(\mu = 0\) in the following. Simulating random variables with \(\mu \neq 0\) can be achieved by (wrapped) translation of variables with \(\mu = 0\).
Thus the target density is \(f(x) \propto e^{\kappa \cos(x)}\). In this section we will use the uniform distribution on \((-\pi, \pi)\) as proposal distribution. It has constant density \(g(x) = (2\pi)^{-1}\), but all we need is, in fact, that \(g(x) \propto 1\). Since \(x \mapsto 1 / \exp(\kappa \cos(x)) = \exp(-\kappa \cos(x))\) attains its minimum \(\exp(-\kappa)\) for \(x = 0\), we find that \[\alpha' e^{\kappa \cos(x)} = e^{\kappa(\cos(x) - 1)} \leq 1,\] with \(\alpha' = \exp(-\kappa)\). The rejection test of the proposal \(Y \sim g\) can therefore be carried out by testing if a uniformly distributed random variable \(U\) on \((0,1)\) satisfies \[U > e^{\kappa(\cos(Y) - 1)}.\]
vMsim_loop <- function(n, kappa) {
y <- numeric(n)
for(i in 1:n) {
reject <- TRUE
while(reject) {
y0 <- runif(1, - pi, pi)
u <- runif(1)
reject <- u > exp(kappa * (cos(y0) - 1))
}
y[i] <- y0
}
y
}
f <- function(x, k) exp(k * cos(x)) / (2 * pi * besselI(k, 0))
x <- vMsim_loop(100000, 0.5)
hist(x, breaks = seq(-pi, pi, length.out = 20), prob = TRUE)
curve(f(x, 0.5), -pi, pi, col = "blue", lwd = 2, add = TRUE)
x <- vMsim_loop(100000, 2)
hist(x, breaks = seq(-pi, pi, length.out = 20), prob = TRUE)
curve(f(x, 2), -pi, pi, col = "blue", lwd = 2, add = TRUE)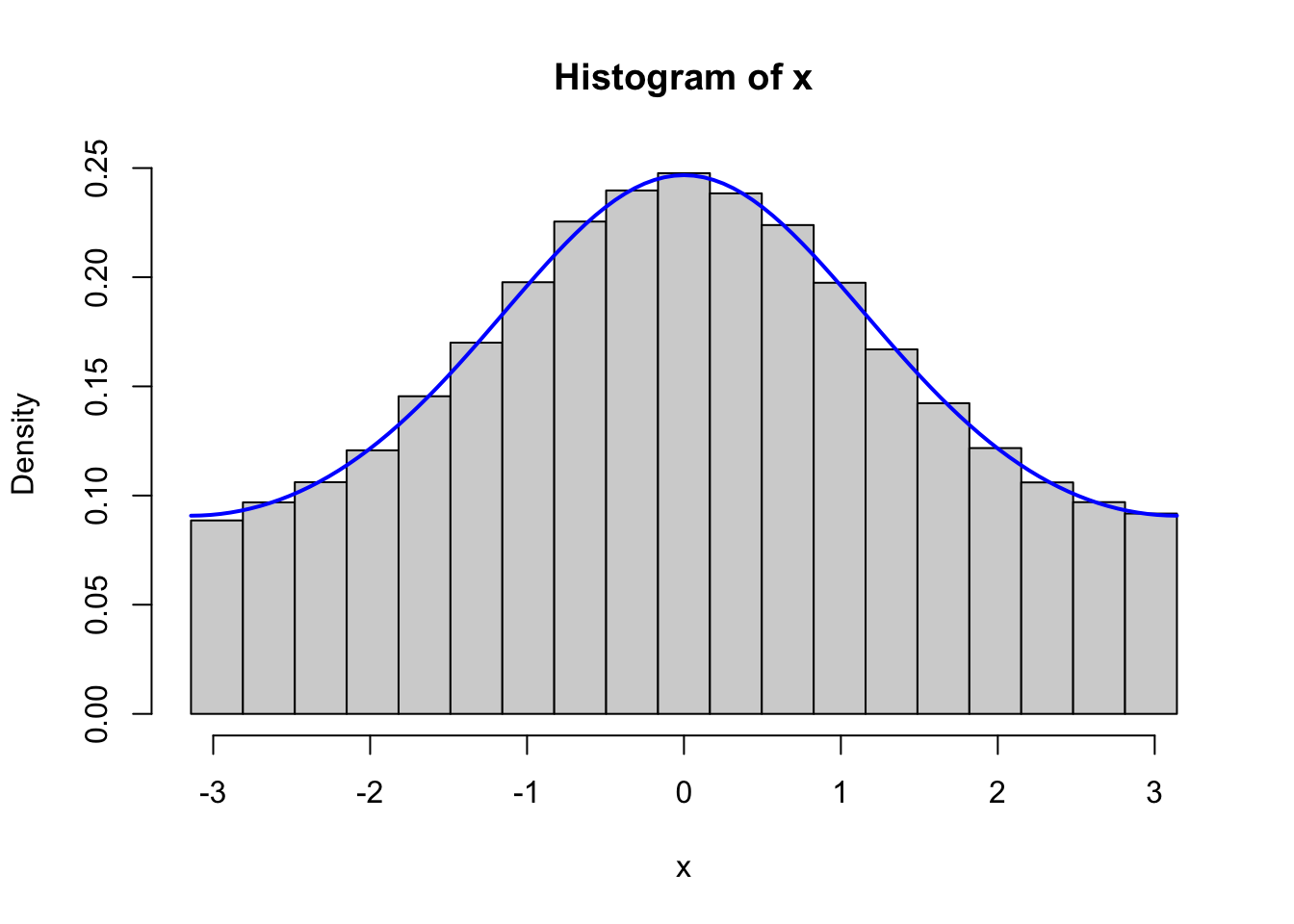
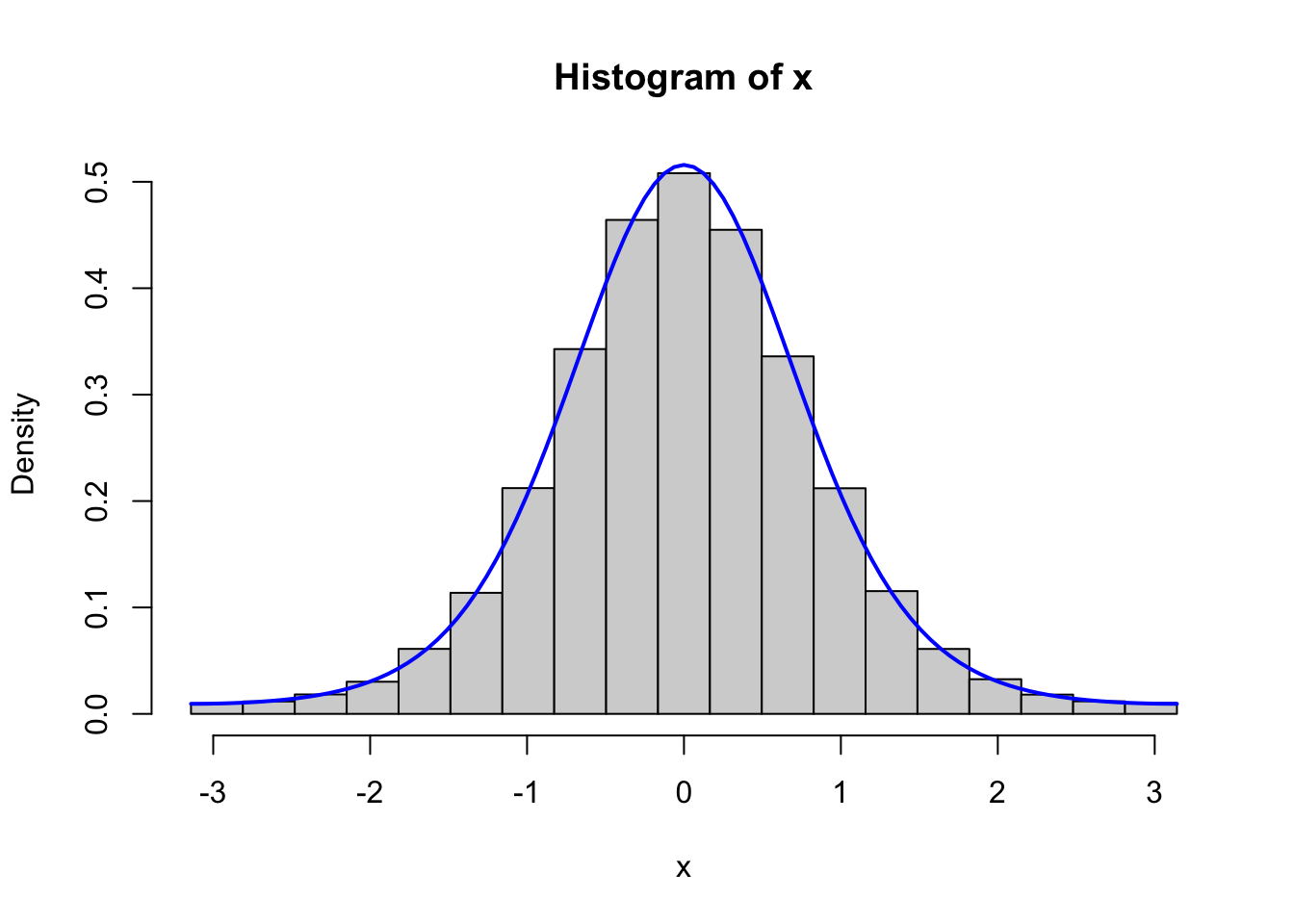
Figure 4.1: Histograms of 100,000 simulated data points from von Mises distributions with parameters \(\kappa = 0.5\) (left) and \(\kappa = 2\) (right). The true densities (blue) are added to the plots.
Figure 4.1 confirms that the implementation simulates from the von Mises distribution.
bench::system_time(vMsim_loop(100000, kappa = 5))## process real
## 1.4s 1.74sThough the implementation can easily simulate 100,000 variables in a couple of seconds, it might still be possible to improve it. To investigate what most of the run time is spent on we use the line profiling tool as implemented in the profvis package, see also Section A.3.1.
p <- profvis::profvis(vMsim_loop(10000, 5))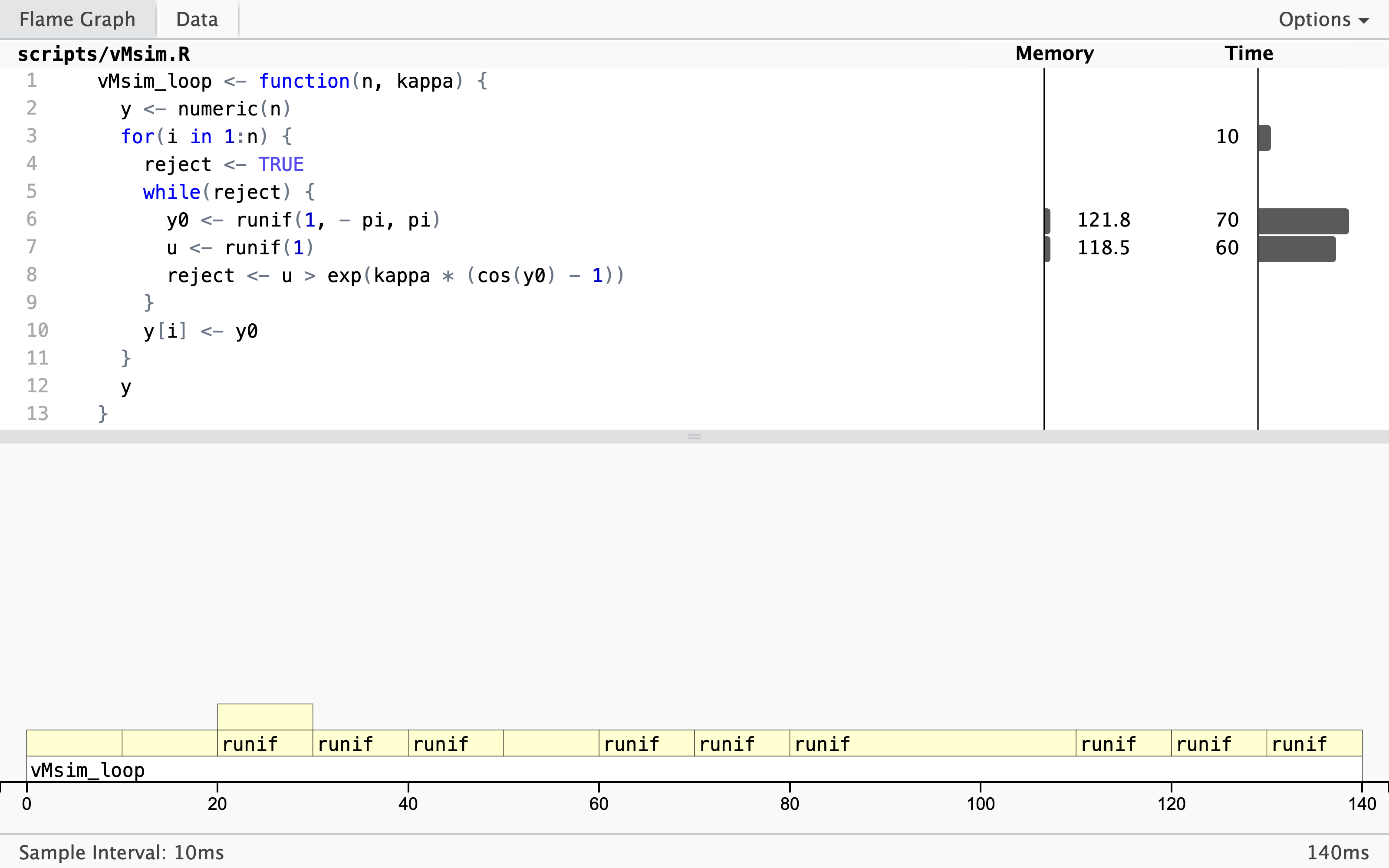
The profiling result shows that almost all the time
is spent on simulating uniformly distributed random variables. It is, perhaps,
expected that this should take some time, but that it takes so much more time
than computing the ratio, say, used for the rejection test is a bit surprising.
What might be even more surprising is the large amount of memory allocation
and deallocation associated with the simulation of the variables. The flame
graph above shows that this has also triggered multiple calls to the the
garbage collector (<GC>).
The culprit is runif() that has some overhead associated with each call.
The function performs much better if called once to return a vector than
if called repeatedly as above to return just single numbers. We could
rewrite the rejection sampler to make better use of runif(), but it would
make the code a bit more complicated because we do not know upfront
how many uniform variables we need. Sections A.2.3 and
A.3 in the appendix shows how to implement caching via
a function factory to mitigate the inefficiency of generating random
numbers sequentially in R, but we will not pursue that idea any
further here.
To write a run time efficient R function we need to do more than just vectorize the generation of random numbers. We need to turn the entire rejection sampler into a vectorized computation. As all computations required are easily vectorized, it is straightforward to do so.
vMsim_random <- function(n, kappa) {
y0 <- runif(n, - pi, pi)
u <- runif(n)
accept <- u <= exp(kappa * (cos(y0) - 1))
y0[accept]
}The only downside of the implementation above is that it returns a
random number of accepted samples instead of n samples. Since we do not
know upfront how many rejections there will be, there is no way around a
loop if we want to convert vMsim_random() into a function that returns
a fixed number of samples. We will need to solve this problem for
several other distributions, so we implement a general solution
that can convert any sampler generating a random number of samples into
a sampler that returns a fixed number of samples.
The solution is a function operator, much like Vectorize(),
that takes a function and returns a function.
The implementation below returns a sampler based on the function argument
rng. The sampler repeatedly calls rng() while adapting the number of proposals
after its first iteration by estimating the acceptance rate. The
two arguments fact and m_min control the adaptation with
defaults ensuring at least 100 proposals and otherwise 20% more
than estimated.
The implementation contains a few additional bells and whistles. First,
the ellipses argument, ..., is used, which captures all arguments to
a function and in this case passes them on via the call rng(m, ...).
Second, for the sake of subsequent usages in Section 4.4.2.
we include the callback argument cb, see also Section A.3.2.
sim_vec <- function(rng, fact = 1.2, m_min = 100) {
force(rng); force(fact); force(m_min)
function(n, ..., cb) {
j <- 0
l <- 0 # The number of accepted samples
y <- list()
while(l < n) {
j <- j + 1
# Adapt the number of proposals
m <- floor(max(fact * (n - l), m_min))
y[[j]] <- rng(m, ...)
l <- l + length(y[[j]])
if (!missing(cb)) cb() # Callback
# Update 'fact' by estimated acceptance probability l / n
if (j == 1) fact <- fact * n / l
}
unlist(y)[1:n]
}
}
vMsim_vec <- sim_vec(vMsim_random)The implementation incrementally grows a list, whose entries contain vectors of accepted samples. It is usually not advisable to dynamically grow objects (vectors or list), as this will unnecessary memory allocation, copying and deallocation. Thus it is better to initialize a vector of the correct size upfront. In this particular case the list will only contain relatively few entries, and it is inconsequential that it is grown dynamically.
Finally, a C++ implementation via Rcpp is given below where the random variables are then again generated one at a time via the C-interface to R’s random number generators. There is no (substantial) overhead of doing so in C++.
#include <Rcpp.h>
using namespace Rcpp;
// [[Rcpp::export]]
NumericVector vMsim_cpp(int n, double kappa) {
NumericVector y(n);
double y0;
bool reject;
for(int i = 0; i < n; ++i) {
do {
y0 = R::runif(- M_PI, M_PI);
reject = R::runif(0, 1) > exp(kappa * (cos(y0) - 1));
} while(reject);
y[i] = y0;
}
return y;
}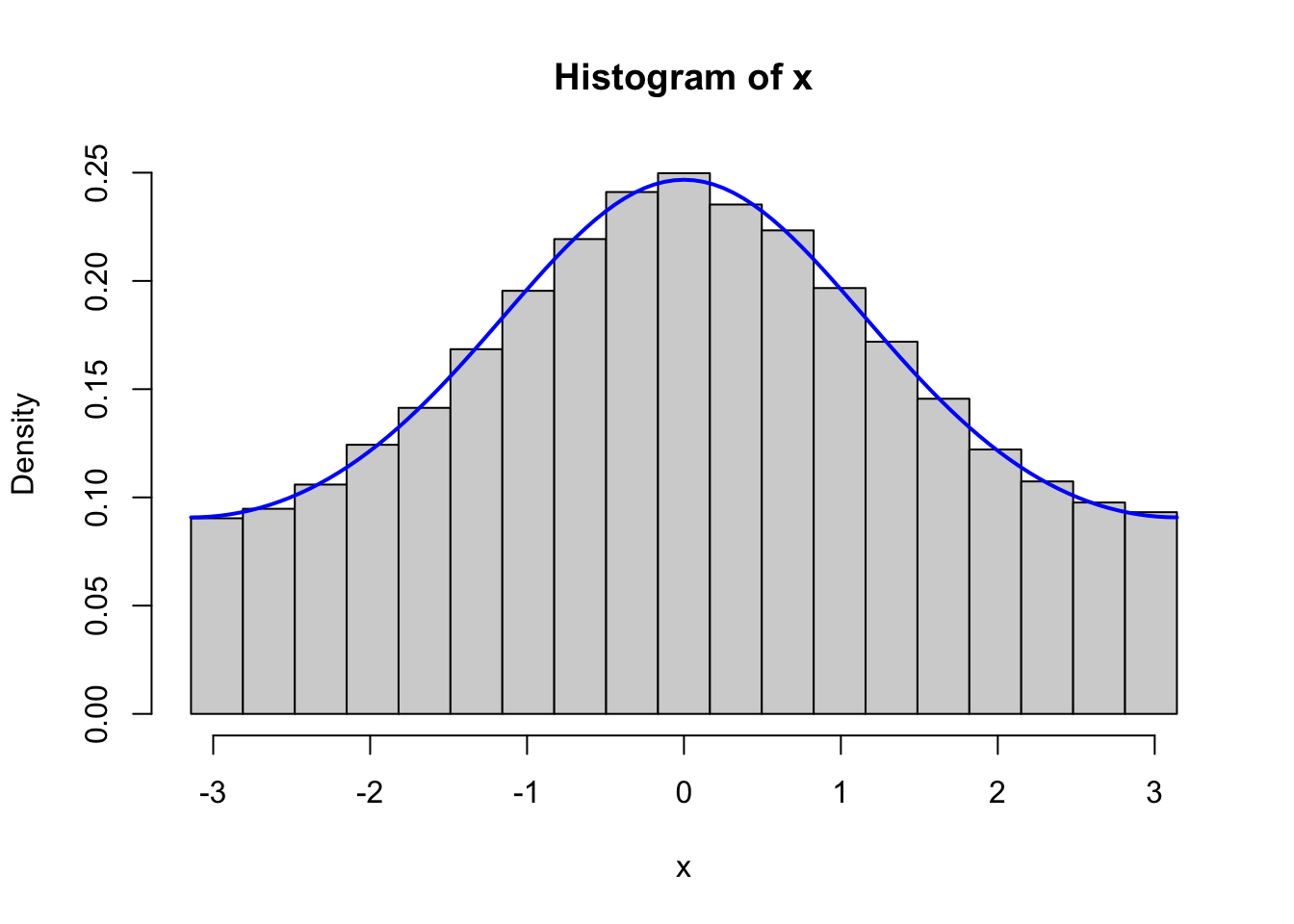
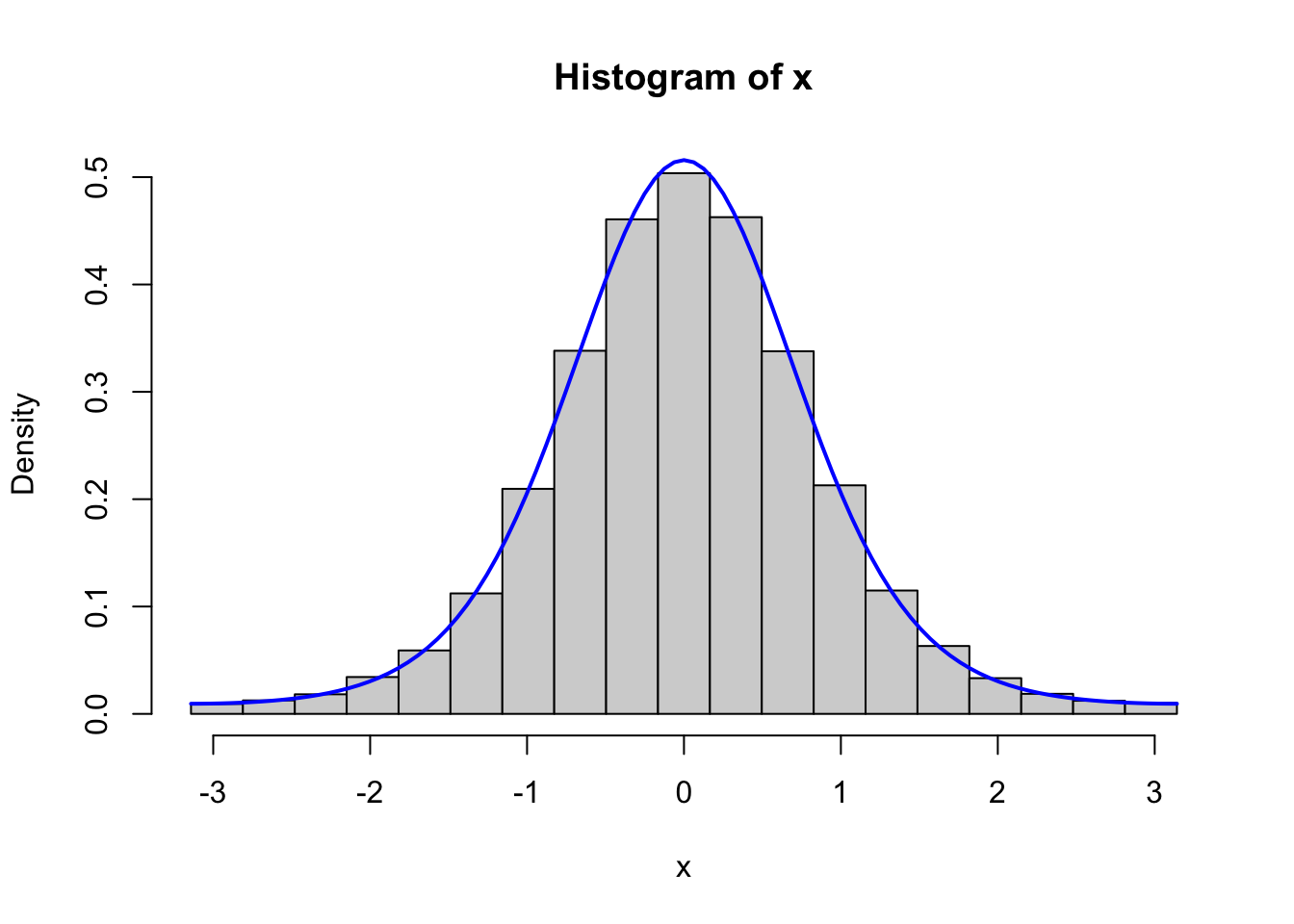
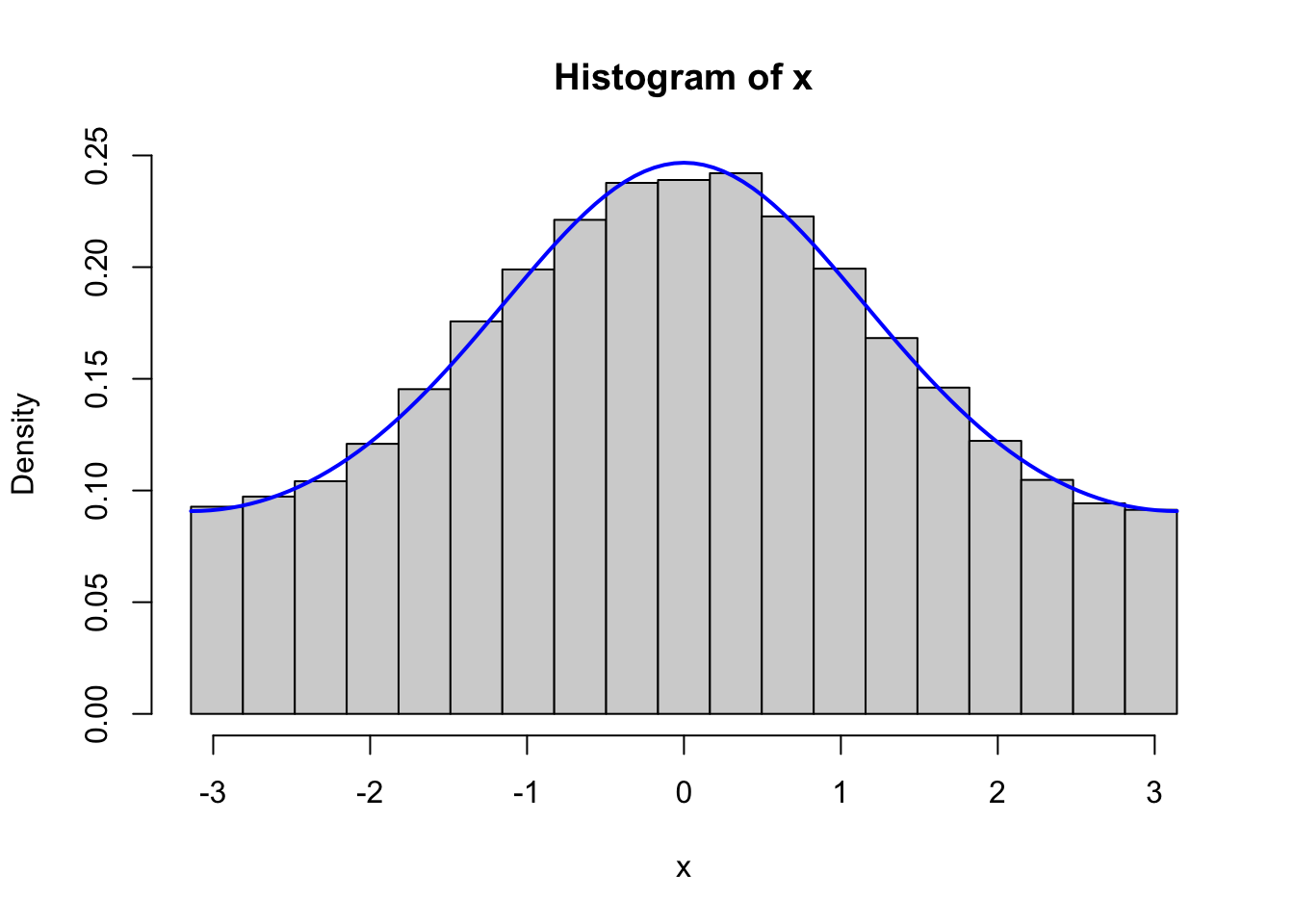
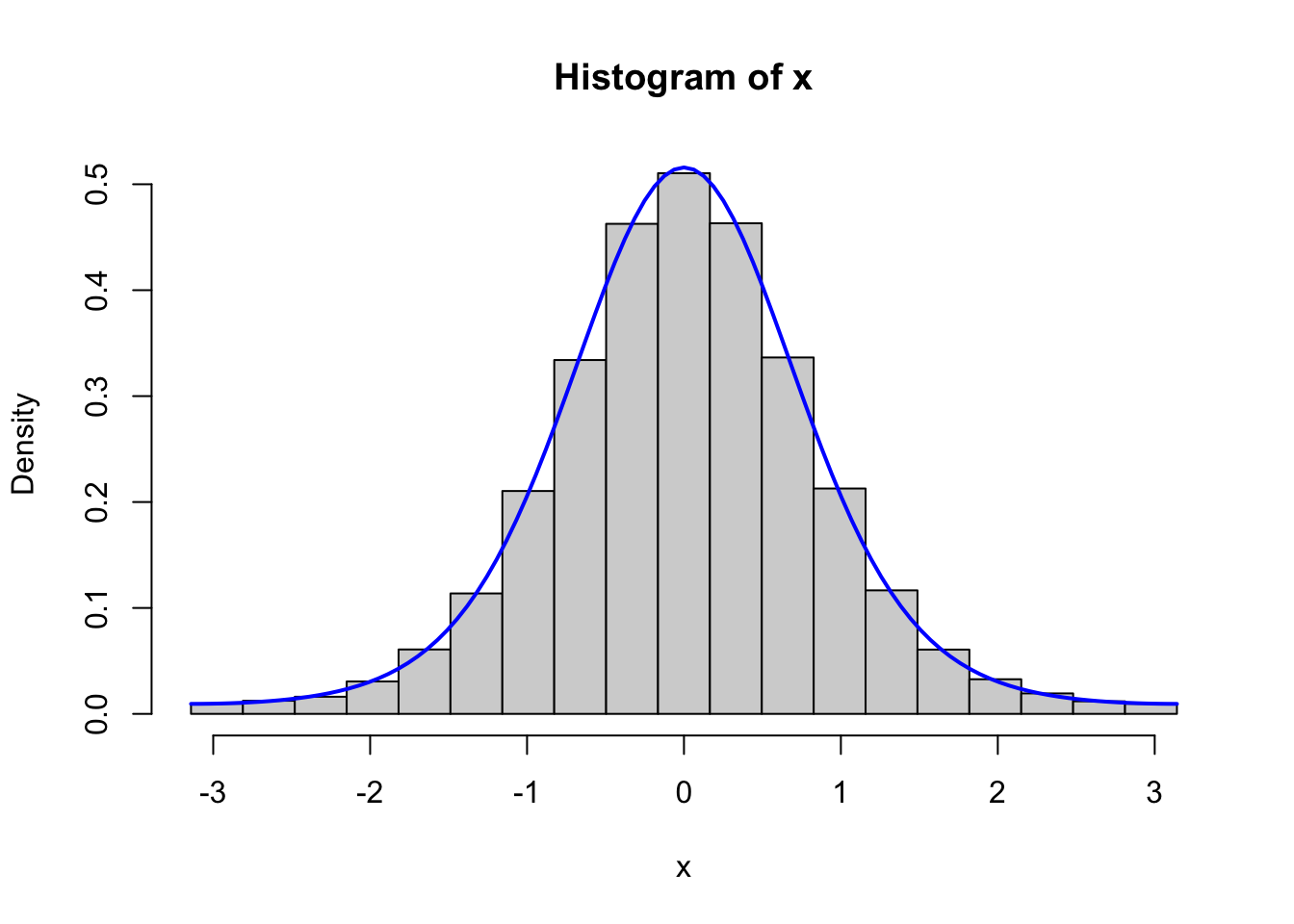
Figure 4.2: Histograms of 100,000 simulated data points from von Mises distributions with parameters \(\kappa = 0.5\) (left) and \(\kappa = 2\) (right), simulated using the Rcpp implementation (top) and the fully vectorized R implementation (bottom).
We should, of course, remember to test that the vectorized implementation as well as the C++ implementation generate variables from the von Mises distribution. Figure 4.2 shows the results from testing both of these implementations, and it confirms that the implementations do simulate from the von Mises distribution.
We conclude by measuring the run time for all three implementations using
the mark() function from the bench package.
bench::mark(
loop = vMsim_loop(1000, kappa = 5),
vec = vMsim_vec(1000, kappa = 5),
cpp = vMsim_cpp(1000, kappa = 5),
check = FALSE
)## # A tibble: 3 × 6
## expression min median `itr/sec` mem_alloc `gc/sec`
## <bch:expr> <bch:tm> <bch:tm> <dbl> <bch:byt> <dbl>
## 1 loop 8.95ms 10.7ms 93.8 26.1MB 7.41
## 2 vec 119.02µs 152µs 6552. 223.6KB 2.10
## 3 cpp 141.7µs 167.3µs 5955. 10.4KB 2.11The C++ implementation is less than a factor 2 faster than the
vectorized R implementation, while it is a factor 70 or so faster than the
first implementation vMsim_loop(). Rejection sampling is a good example
of an algorithm for which a naive loop-based R implementation
performs rather poorly in terms of run time, while a vectorized
implementation is competitive with an Rcpp implementation.
4.3.2 Gamma distribution
It may be possible to find a suitable envelope of the density for the gamma distribution on \((0, \infty)\), but it turns out that there is a very efficient rejection sampler of a non-standard distribution that can be transformed into a gamma distribution by a simple transformation.
Let \(t(y) = a(1 + by)^3\) for \(y \in (-b^{-1}, \infty)\), then \(t(Y) \sim \Gamma(r,1)\) if \(r \geq 1\) and \(Y\) has density \[f(y) \propto t(y)^{r-1}t'(y) e^{-t(y)} = e^{(r-1)\log t(y) + \log t'(y) - t(y)}.\]
The proof of this follows from a simple univariate density transformation theorem, but see also the original paper Marsaglia and Tsang (2000) that proposed the rejection sampler discussed in this section. The density \(f\) will be the target density for a rejection sampler.
With \[f(y) \propto e^{(r-1)\log t(y) + \log t'(y) - t(y)},\] \(a = r - 1/3\) and \(b = 1/(3 \sqrt{a})\) \[f(y) \propto e^{a \log t(y)/a - t(y) + a \log a} \propto \underbrace{e^{a \log t(y)/a - t(y) + a}}_{q(y)}.\]
An analysis of \(w(y) := - y^2/2 - \log q(y)\) shows that it is convex on \((-b^{-1}, \infty)\) and it attains its minimum in \(0\) with \(w(0) = 0\), whence \[q(y) \leq e^{-y^2/2}.\] This gives us an envelope expressed in terms of unnormalized densities with \(\alpha' = 1\).
The implementation of a rejection sampler based on this analysis is relatively
straightforward. The rejection sampler will simulate from the distribution
with density \(f\) by simulating from the Gaussian distribution (the envelope).
For the rejection step we need to implement \(q\). Finally, we also need
to implement \(t\) to transform the result from the rejection sampler to be
gamma distributed. The rejection sampler is otherwise implemented as for
the vectorized von Mises distribution except that we lower fact to 1.1.
By doing so the initial batch of proposals will be 10% larger than the
desired sample size, and a second batch is rarely generated if the acceptance
rate is above 91%.
## r >= 1
tfun <- function(y, a) {
b <- 1 / (3 * sqrt(a))
(y > -1/b) * a * (1 + b * y)^3 ## 0 when y <= -1/b
}
qfun <- function(y, r) {
a <- r - 1/3
tval <- tfun(y, a)
exp(a * log(tval / a) - tval + a)
}
gammasim_random <- function(n, r) {
y0 <- rnorm(n)
u <- runif(n)
accept <- u <= qfun(y0, r) * exp(y0^2/2)
y <- y0[accept]
tfun(y, r - 1/3)
}
gammasim <- sim_vec(gammasim_random, fact = 1.1)We test the implementation by simulating \(100,000\) values with parameters \(r = 8\) as well as \(r = 1\) and compare the resulting histograms to the respective theoretical densities.
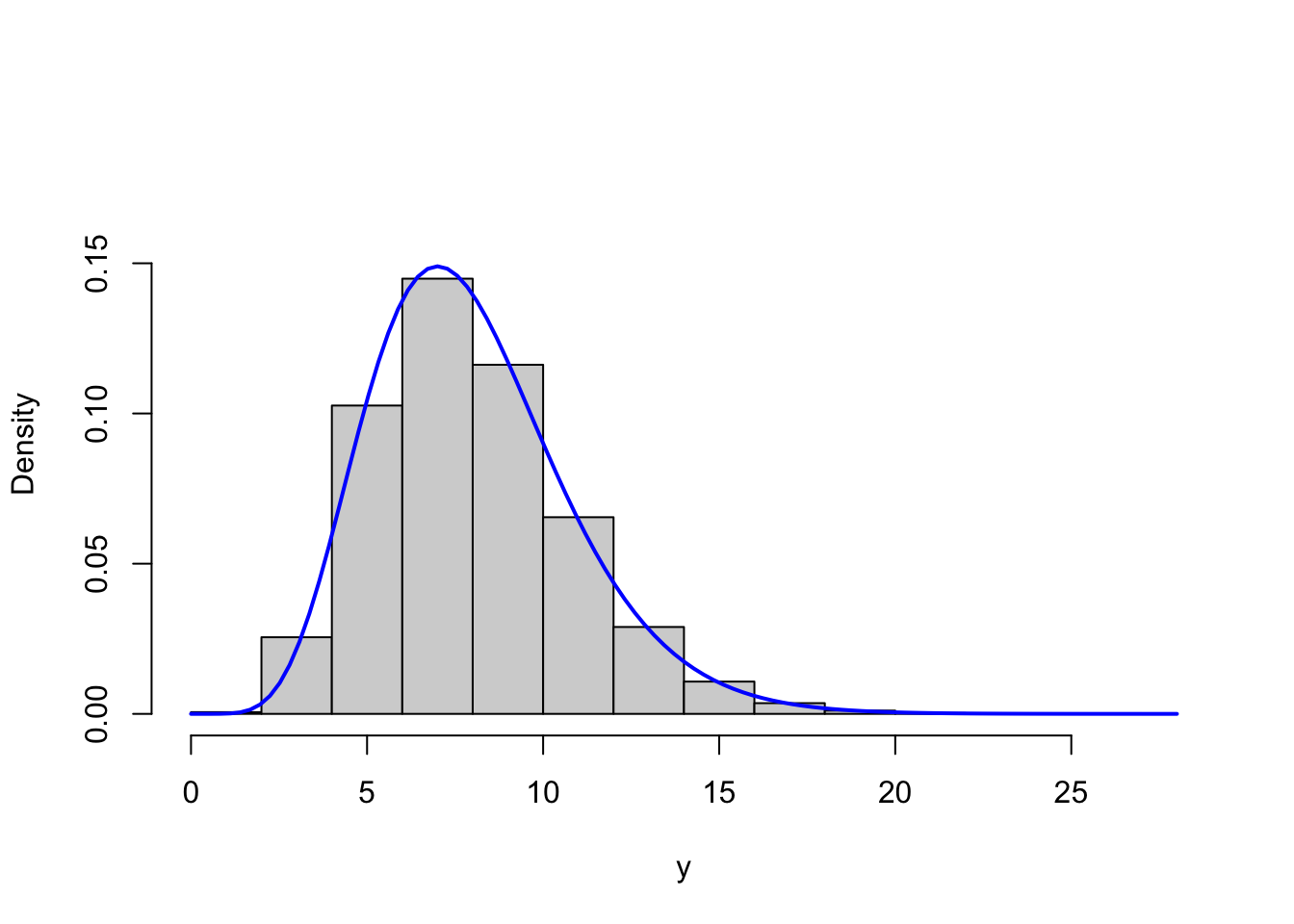
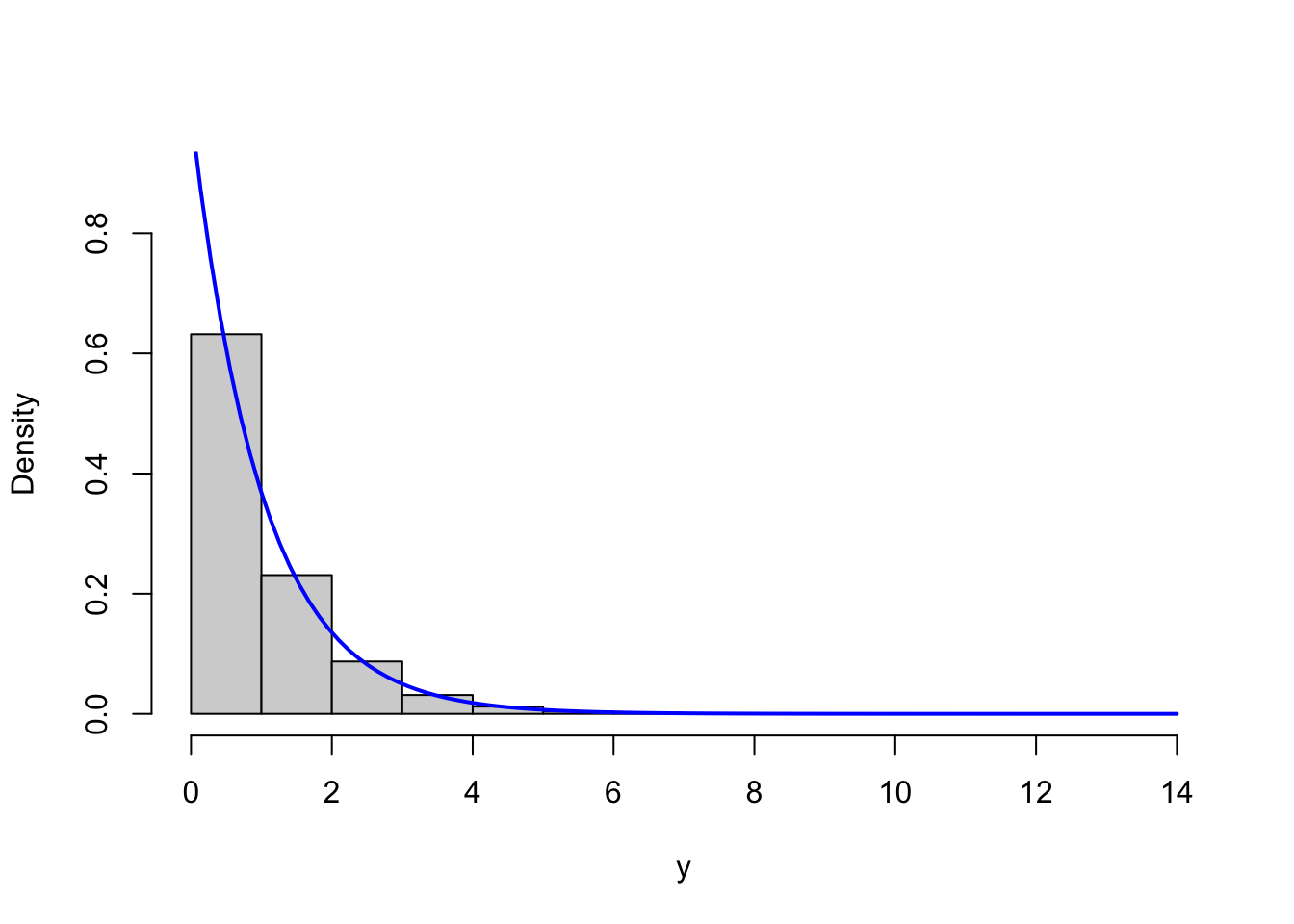
Figure 4.3: Histograms of simulated gamma distributed variables with shape parameters \(r = 8\) (left) and \(r = 1\) (right) with corresponding theoretical densities (blue).
Though this is only a simple and informal test, it indicates that the implementation correctly simulates from the gamma distribution.
Rejection sampling can be computationally expensive if many samples are rejected. A very tight envelope will lead to fewer rejections, while a loose envelope will lead to many rejections. To investigate the acceptance rate we use the the callback argument with a tracer. The tracer computes an estimate of the acceptance rate from the first (and in most cases only) iteration in the loop.
gammasim_tracer <- tracer(
"alpha",
# alpha is the estimated acceptance rate
expr = quote(alpha <- l / m)
)
y <- gammasim(100000, 16, cb = gammasim_tracer$trace)
y <- gammasim(100000, 8, cb = gammasim_tracer$trace)
y <- gammasim(100000, 4, cb = gammasim_tracer$trace)
y <- gammasim(100000, 1, cb = gammasim_tracer$trace)## n = 1: alpha = 0.9982;
## n = 2: alpha = 0.9961;
## n = 3: alpha = 0.9919;
## n = 4: alpha = 0.9523;We observe that the acceptance rates are large with \(r = 1\) being the worst case but still with more than 95% acceptances For the other cases the acceptance rates are all above 99%, thus rejection is rare.
A visual comparison of \(q\) to the (unnormalized) Gaussian density also shows that the two (unnormalized) densities are very close except in the tails where there is very little probability mass.
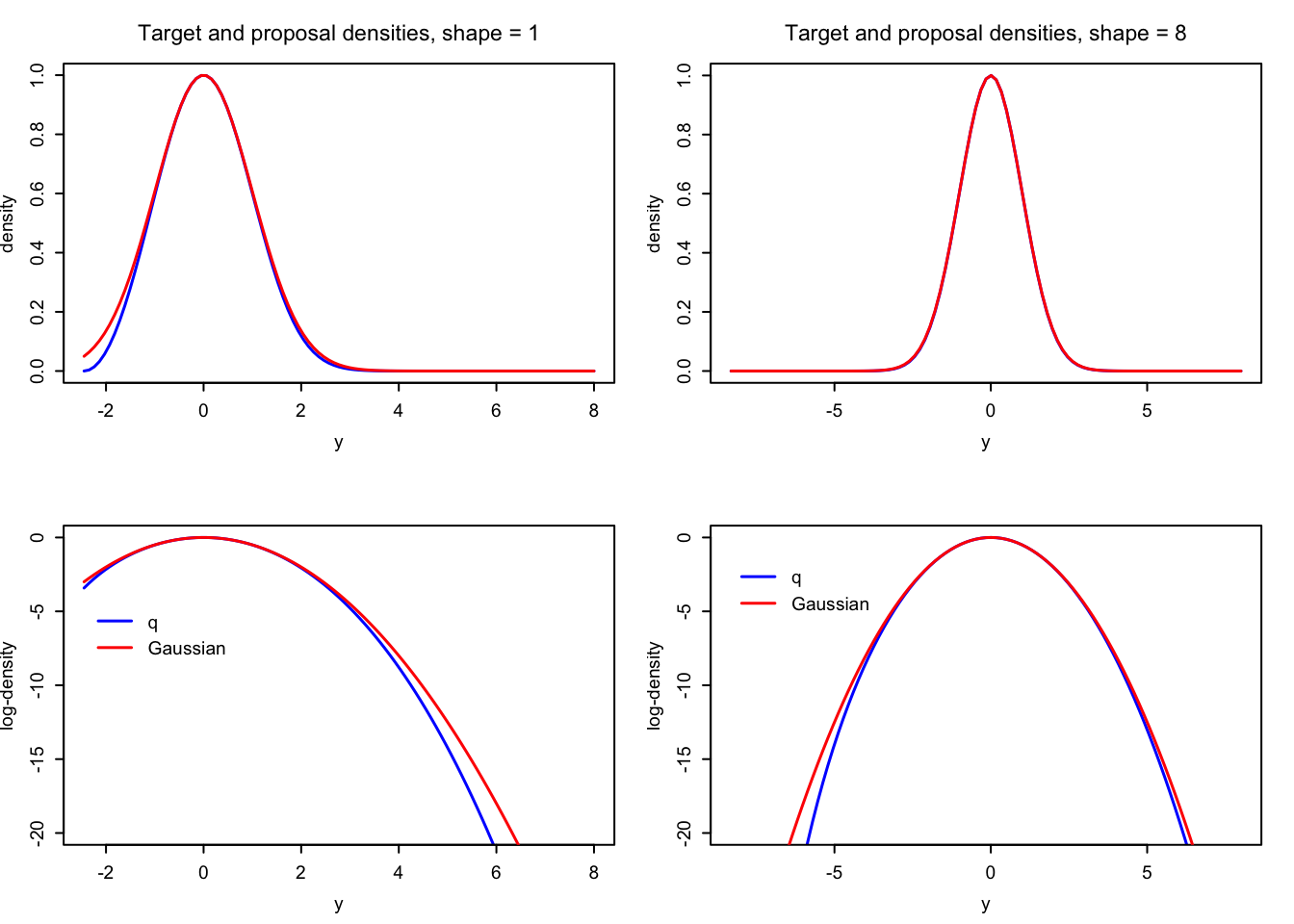
Figure 4.4: Comparisons of the Gaussian proposal (red) and the target density (blue) used for simulating gamma distributed variables via a transformation.
4.4 Adaptive envelopes
A good envelope should be tight, meaning that \(\alpha\) is close to one, it should be fast to simulate from and have a density that is fast to evaluate. It is not obvious how to find such an envelope for an arbitrary target density \(f\).
This section develops a general scheme for the construction of envelopes for all log-concave target densities. This is a special class of densities, but it is not uncommon in practice. The scheme can also be extended to work for some densities that have combinations of log-concave and log-convex behaviors. The same idea used for constructing envelopes can be used to bound \(f\) from below. The accept-reject step can then avoid many evaluations of \(f\), which is beneficial if \(f\) is computationally expensive to evaluate.
The key idea of the scheme is to bound the log-density by piecewise affine functions. This is particularly easy to do if the density is log-concave. The scheme leads to analytically manageable formulas for the envelope, its corresponding distribution function and its inverse, and as a result it is fast to simulate proposals and compute the envelope as needed in the accept-reject step.
The scheme requires the choice of a finite number of points to determine the affine bounds. For any given choice of points the scheme adapts the envelope to the target density automatically. It is possible to implement a fully adaptive scheme that doesn’t even require the choice of points but initializes and updates the points dynamically as more and more rejection samples are computed. In this section the focus is on the scheme with a given and fixed number of points.
For a continuously differentiable, strictly positive and log-concave target on an open interval \(I \subseteq \mathbb{R}\) it holds that \[\log(f(x)) \leq \frac{f'(x_0)}{f(x_0)}(x - x_0) + \log(f(x_0))\] for any \(x, x_0 \in I\).
Let \(x_1 < x_2 < \ldots < x_{m} \in I\) and let \(I_1, \ldots, I_m \subseteq I\) be intervals that form a partition of \(I\) such that \(x_i \in I_i\). Defining \[a_i = (\log(f(x_i)))' = \frac{f'(x_i)}{f(x_i)} \quad \text{and} \quad b_i = \log(f(x_i)) - \alpha_i x_i\] we find the upper bound \[\log(f(x)) \leq V(x) = \sum_{i=1}^m (a_i x + b_i) 1_{I_i}(x),\] or \[f(x) \leq e^{V(x)}.\] Note that by the log-concavity of \(f\), \(a_1 \geq a_2 \geq \ldots \geq a_m\). The upper bound is integrable over \(I\) if either \(a_1 > 0\) and \(a_m < 0\), or \(a_m < 0\) and \(I\) is bounded to the left, or \(a_1 > 0\) and \(I\) is bounded to the right. In any of these cases we define \[c = \int_I e^{V(x)} \mathrm{d} x < \infty\] and \(g(x) = c^{-1} \exp(V(x))\), and we find that with \(\alpha = c^{-1}\) then \(\alpha f \leq g\) and \(g\) is an envelope of \(f\). Note that it is actually not necessary to compute \(c\) (or \(\alpha\)) to implement the rejection step in the rejection sampler, but that \(c\) is needed for simulating from \(g\) as described below. We will assume in the following that \(c < \infty\).
The intervals \(I_i\) have not been specified, and we could, in fact, implement rejection sampling with any choice of intervals fulfilling the conditions above. But in the interest of maximizing \(\alpha\) (minimizing \(c\)) and thus minimizing the rejection frequency, we should choose \(I_i\) so that \(a_i x + b_i\) is minimal over \(I_i\) among all the affine upper bounds. This will result in the tightest envelope. This means that for \(i = 1, \ldots, m - 1\), \(I_i = (z_{i-1}, z_i]\) with \(z_i\) the point where \(a_i x + b_i\) and \(a_{i+1} x + b_{i+1}\) intersect. We find that the solution of \[a_i x + b_i = a_{i+1} x + b_{i+1}\] is \[z_i = \frac{b_{i+1} - b_i}{a_i - a_{i+1}}\] provided that \(a_{i+1} > a_i\). The two extremes, \(z_0\) and \(z_m\), are chosen as the endpoints of \(I\) and may be \(- \infty\) and \(+ \infty\), respectively.
One way to simulate from such envelopes is by transformation of uniform random variables by the inverse distribution function. It requires a little bookkeeping, but is otherwise straightforward. Define for \(x \in I_i\) \[F_i(x) = \int_{z_{i-1}}^x e^{a_i z + b_i} \mathrm{d} z,\] and let \(R_i = F_i(z_i)\). Then \(c = \sum_{i=1}^m R_i\), and if we define \(Q_i = \sum_{k=1}^{i} R_k\) for \(i = 0, \ldots, m\) the inverse of the distribution function in \(q\) is given as the solution to the equation \[F_i(x) = cq - Q_{i-1}, \qquad Q_{i-1} < cq \leq Q_{i}.\] That is, for a given \(q \in (0, 1)\), first determine which interval \((Q_{i-1}, Q_{i}]\) that \(c q\) falls into, and then solve the corresponding equation. Observe that when \(a_i \neq 0\), \[F_i(x) = \frac{1}{a_i}e^{b_i}\left(e^{a_i x} - e^{a_i z_{i-1}}\right).\]
4.4.1 Beta distribution
To illustrate the envelope construction above for a simple log-concave density we consider the Beta distribution on \((0, 1)\) with shape parameters \(\geq 1\). This distribution has density \[f(x) \propto x^{\alpha - 1}(1-x)^{\beta - 1},\] which is log-concave (when the shape parameters are greater than one). We implement the rejection sampling algorithm for this density with the adaptive envelope using two points.
Betasim_random <- function(n, x1, x2, alpha, beta) {
lf <- function(x) (alpha - 1) * log(x) + (beta - 1) * log(1 - x)
lf_deriv <- function(x) (alpha - 1)/x - (beta - 1)/(1 - x)
a1 <- lf_deriv(x1)
a2 <- lf_deriv(x2)
if(a1 == 0 || a2 == 0 || a1 - a2 == 0)
stop("\nThe implementation requires a_1 and a_2 different
and both different from zero. Choose different values of x_1 and x_2.")
b1 <- lf(x1) - a1 * x1
b2 <- lf(x2) - a2 * x2
z1 <- (b2 - b1) / (a1 - a2)
Q1 <- exp(b1) * (exp(a1 * z1) - 1) / a1
c <- Q1 + exp(b2) * (exp(a2 * 1) - exp(a2 * z1)) / a2
y <- numeric(n)
accept <- logical(n)
u0 <- c * runif(n)
u <- runif(n)
I <- u0 < Q1
y[I] <- log(a1 * exp(-b1) * u0[I] + 1) / a1
accept[I] <- u[I] <= exp(lf(y[I]) - a1 * y[I] - b1)
y[!I] <- log(a2 * exp(-b2) * (u0[!I] - Q1) + exp(a2 * z1)) / a2
accept[!I] <- u[!I] <= exp(lf(y[!I]) - a2 * y[!I] - b2)
y[accept]
}
Betasim <- sim_vec(Betasim_random)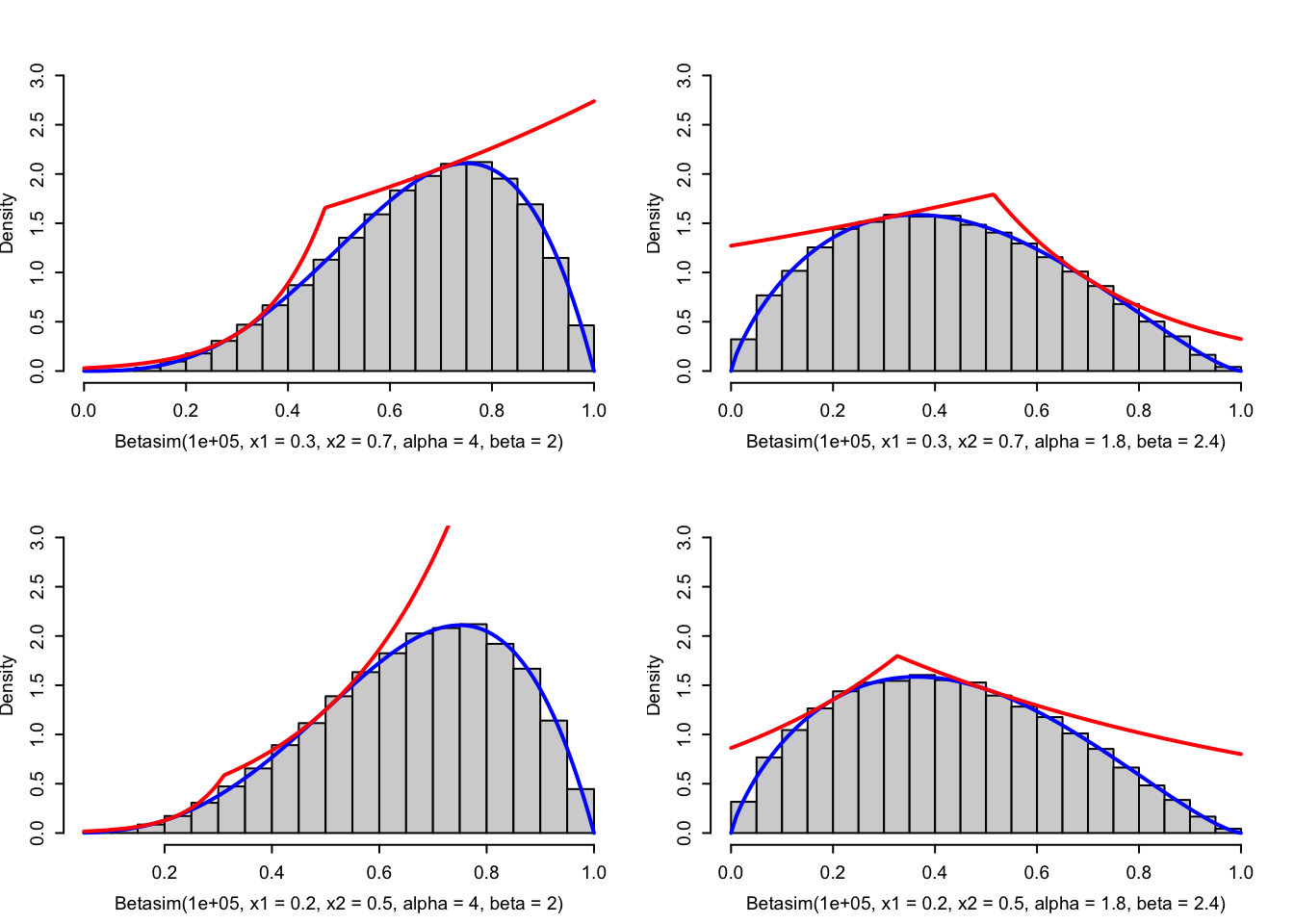
Figure 4.5: Histograms of simulated variables from Beta distributions using the rejection sampler with the adaptive envelope based on log-concavity. The true density (blue) and the envelope (red) are added to the plots.
Note that as a safeguard we implemented a test on the \(a_i\)-s to check that the formulas used are actually meaningful, specifically that there are no divisions by zero.
Betasim(1, x1 = 0.25, x2 = 0.75, alpha = 4, beta = 2) ## Error in rng(m, ...): ## The implementation requires a_1 and a_2
different ## and both different from zero. Choose different values of
x_1 and x_2.
Betasim(1, x1 = 0.2, x2 = 0.75, alpha = 4, beta = 2) ## Error in rng(m, ...): ## The implementation requires a_1 and a_2
different ## and both different from zero. Choose different values of
x_1 and x_2.
Betasim(1, x1 = 0.2, x2 = 0.8, alpha = 4, beta = 2) ## [1] 0.36924.4.2 von Mises distribution
The von Mises rejection sampler in Section 4.3.1 used the uniform distribution as proposal distribution. As it turns out, the uniform density is not a particularly tight envelope. We illustrate this by studying the acceptance rate for our previous implementation.
vMsim_tracer <- tracer(
c("r", "l", "mm"),
N = 0,
time = FALSE,
expr = quote({r <- ..1; if (j == 1) mm <- m else mm <- mm + m})
)
y <- vMsim_vec(10000, 0.1, cb = vMsim_tracer$trace)
y <- vMsim_vec(10000, 0.5, cb = vMsim_tracer$trace)
y <- vMsim_vec(10000, 2, cb = vMsim_tracer$trace)
y <- vMsim_vec(10000, 5, cb = vMsim_tracer$trace)
trace_sum <- summary(vMsim_tracer)
trace_sum$alpha = trace_sum$l / trace_sum$mm
trace_sum[trace_sum$l >= 10000, ]## l r mm alpha
## 1 10865 0.1 12000 0.9054
## 4 10037 0.5 15542 0.6458
## 8 10026 2.0 32251 0.3109
## 10 10010 5.0 53691 0.1864The acceptance rate decreases with \(\kappa\) and is fairly small unless \(\kappa\) is small. For \(\kappa = 5\) less than 20% of the proposals are accepted, and simulating \(n = 10,000\) von Mises distributed variables thus requires the simulation of more than \(50,000\) variables from the proposal.
The von Mises density is, unfortunately, not log-concave on \((-\pi, \pi)\), but it is on \((-\pi/2, \pi/2)\). It is, furthermore, log-convex on \((-\pi, -\pi/2)\) as well as \((\pi/2, \pi)\), which implies that on these two intervals the log-density is below the corresponding chords. These chords can be pieced together with tangents to give an envelope. We first implement the algorithm that returns a random length vector.
vMsim_adapt_random <- function(n, x1, x2, kappa) {
lf <- function(x) kappa * cos(x)
lf_deriv <- function(x) - kappa * sin(x)
a1 <- 2 * kappa / pi
a2 <- lf_deriv(x1)
a3 <- lf_deriv(x2)
a4 <- - a1
b1 <- kappa
b2 <- lf(x1) - a2 * x1
b3 <- lf(x2) - a3 * x2
b4 <- kappa
z0 <- -pi
z1 <- -pi/2
z2 <- (b3 - b2) / (a2 - a3)
z3 <- pi/2
z4 <- pi
Q1 <- exp(b1) * (exp(a1 * z1) - exp(a1 * z0)) / a1
Q2 <- Q1 + exp(b2) * (exp(a2 * z2) - exp(a2 * z1)) / a2
Q3 <- Q2 + exp(b3) * (exp(a3 * z3) - exp(a3 * z2)) / a3
c <- Q3 + exp(b4) * (exp(a4 * z4) - exp(a4 * z3)) / a4
u0 <- c * runif(n)
u <- runif(n)
I1 <- (u0 < Q1)
I2 <- (u0 >= Q1) & (u0 < Q2)
I3 <- (u0 >= Q2) & (u0 < Q3)
I4 <- (u0 >= Q3)
y <- numeric(n)
accept <- logical(n)
y[I1] <- log(a1 * exp(-b1) * u0[I1] + exp(a1 * z0)) / a1
accept[I1] <- u[I1] <= exp(lf(y[I1] ) - a1 * y[I1] - b1)
y[I2] <- log(a2 * exp(-b2) * (u0[I2] - Q1) + exp(a2 * z1)) / a2
accept[I2] <- u[I2] <= exp(lf(y[I2]) - a2 * y[I2] - b2)
y[I3] <- log(a3 * exp(-b3) * (u0[I3] - Q2) + exp(a3 * z2)) / a3
accept[I3] <- u[I3] <= exp(lf(y[I3]) - a3 * y[I3] - b3)
y[I4] <- log(a4 * exp(-b4) * (u0[I4] - Q3) + exp(a4 * z3)) / a4
accept[I4] <- u[I4] <= exp(lf(y[I4]) - a4 * y[I4] - b4)
y[accept]
}Then we turn the implementation into a function that returns a fixed number of samples, and using the tracer we estimate the acceptance rates for four different combinations of parameters and partition points.
vMsim_adapt <- sim_vec(vMsim_adapt_random)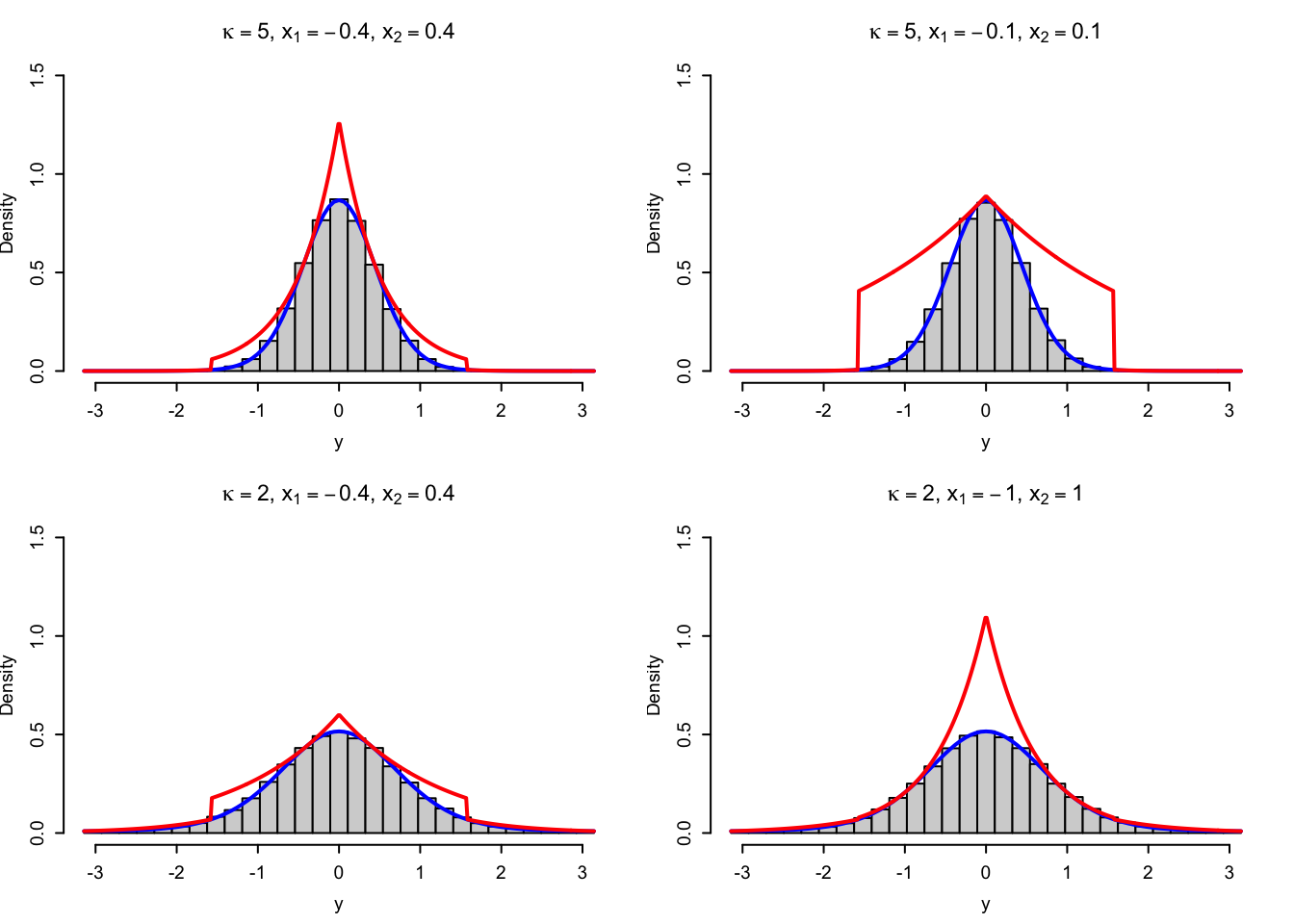
Figure 4.6: Histograms of simulated variables from von Mises distributions using the rejection sampler with the adaptive envelope based on a combination of log-concavity and log-convexity. The true density (blue) and the envelope (red) are added to the plots.
vMsim_tracer$clear()
y <- vMsim_adapt(10000, -0.4, 0.4, 5, cb = vMsim_tracer$trace)
y <- vMsim_adapt(10000, -0.1, 0.1, 5, cb = vMsim_tracer$trace)
y <- vMsim_adapt(10000, -0.4, 0.4, 2, cb = vMsim_tracer$trace)
y <- vMsim_adapt(10000, -1, 1, 2, cb = vMsim_tracer$trace)## l r mm alpha
## 2 10018 -0.4 12605 0.7948
## 5 10000 -0.1 19314 0.5178
## 6 10087 -0.4 12000 0.8406
## 9 10039 -1.0 13333 0.7529We see that compared to using the uniform density as envelope, these adaptive envelopes are generally tighter and leads to fewer rejections. Even tighter envelopes are possible by using more than four intervals, but it is, of course, always a good question how the added complexity and bookkeeping induced by using more advanced and adaptive envelopes affect run time. It is even a good question if our current adaptive implementation will outperform our much simpler implementation that used the uniform envelope.
bench::mark(
adapt1 = vMsim_adapt(100, -1, 1, 5),
adapt2 = vMsim_adapt(100, -0.4, 0.4, 5),
adapt3 = vMsim_adapt(100, -0.2, 0.2, 5),
adapt4 = vMsim_adapt(100, -0.1, 0.1, 5),
vec = vMsim_vec(100, 5),
check = FALSE
)## # A tibble: 5 × 6
## expression min median `itr/sec` mem_alloc `gc/sec`
## <bch:expr> <bch:tm> <bch:tm> <dbl> <bch:byt> <dbl>
## 1 adapt1 42.6µs 64.6µs 15514. 86.7KB 4.84
## 2 adapt2 22.4µs 47.8µs 20782. 69.9KB 2.34
## 3 adapt3 42µs 47.8µs 20289. 69.1KB 5.12
## 4 adapt4 42µs 47.6µs 20559. 68.7KB 2.25
## 5 vec 16.7µs 24.8µs 38796. 31.6KB 3.88The results from the benchmark show that the adaptive implementation has run time comparable to but slightly slower than using the uniform proposal. With \(x_1 = -0.4\) and \(x_2 = 0.4\) and \(\kappa = 5\) we found above that the acceptance rate was about 80% with the adaptive envelope, while it was below 20% when using the uniform envelope. A naive computation would thus suggest a speedup of a factor 4, but using the adaptive envelope there is actually no speedup with the current implementation. It is left as an exercise to implement the adaptive rejection sampler in Rcpp to test if any speedup can be obtained in this way.
The benchmarks above show that when comparing algorithms and their implementations we should not get too focused on surrogate performance quantities. The acceptance rate is a surrogate for actual run time. It might in principle be of interest to increase this probability, but if it is at the expense of additional computations it might not be worth the effort in terms of actual run time.
4.5 Exercises
4.5.1 Rejection sampling of Gaussian random variables
This exercise is on rejection sampling from the Gaussian distribution by using the Laplace distribution as an envelope. Recall that the Laplace distribution has density \[g(x) = \frac{1}{2} e^{-|x|}\] for \(x \in \mathbb{R}\).
Note that if \(X\) and \(Y\) are independent and exponentially distributed with mean one, then \(X - Y\) has a Laplace distribution. This gives a way to easily sample from the Laplace distribution.
Exercise 4.1 Implement rejection sampling from the standard Gaussian distribution with density \[f(x) = \frac{1}{\sqrt{2\pi}} e^{- x^2 / 2}\] by simulating Laplace random variables as differences of exponentially distributed random variables. Test the implementation by computing the variance of the Gaussian distribution as an MC estimate and by comparing directly with the Gaussian distribution using histograms and QQ-plots.
Exercise 4.2 Implement simulation from the Laplace distribution by transforming a uniform random variable by the inverse distribution function. Use this method together with the rejection sampler you implemented in Exercise 4.1
Note: The Laplace distribution can be seen as a simple version of the adaptive envelopes suggested in Section 4.4.